reationists occasionally charge that
evolution is useless as a scientific theory because it
produces no practical benefits and has no relevance to
daily life. However, the evidence of biology alone shows
that this claim is untrue. There are numerous natural
phenomena for which evolution gives us a sound theoretical
underpinning. To name just one, the observed development of
resistance - to insecticides in crop pests, to antibiotics
in bacteria, to chemotherapy in cancer cells, and to
anti-retroviral drugs in viruses such as HIV - is a
straightforward consequence of the laws of mutation and
selection, and understanding these principles has helped us
to craft strategies for dealing with these harmful
organisms. The evolutionary postulate of common descent has
aided the development of new medical drugs and techniques
by giving researchers a good idea of which organisms they
should experiment on to obtain results that are most likely
to be relevant to humans. Finally, the principle of
selective breeding has been used to great effect by humans
to create customized organisms unlike anything found in
nature for their own benefit. The canonical example, of
course, is the many varieties of domesticated dogs (breeds
as diverse as bulldogs, chihuahuas and dachshunds have been
produced from wolves in only a few thousand years), but
less well-known examples include cultivated maize (very
different from its wild relatives, none of which have the
familiar "ears" of human-grown corn), goldfish (like dogs,
we have bred varieties that look dramatically different
from the wild type), and dairy cows (with immense udders
far larger than would be required just for nourishing
offspring).
Critics might charge that creationists can explain these
things without recourse to evolution. For example,
creationists often explain the development of resistance to
antibiotic agents in bacteria, or the changes wrought in
domesticated animals by artificial selection, by presuming
that God decided to create organisms in fixed groups,
called "kinds" or baramin. Though natural
microevolution or human-guided artificial selection can
bring about different varieties within the originally
created "dog-kind," or "cow-kind," or "bacteria-kind" (!),
no amount of time or genetic change can transform one
"kind" into another. However, exactly how the creationists
determine what a "kind" is, or what mechanism prevents
living things from evolving beyond its boundaries, is
invariably never explained.
But in the last few decades, the continuing advance of
modern technology has brought about something new.
Evolution is now producing practical benefits in a very
different field, and this time, the creationists cannot
claim that their explanation fits the facts just as well.
This field is computer science, and the benefits come from
a programming strategy called genetic algorithms.
This essay will explain what genetic algorithms are and
will show how they are relevant to the
evolution/creationism debate.
What is a genetic algorithm?
|
|
Concisely stated, a genetic algorithm (or GA for short)
is a programming technique that mimics biological evolution
as a problem-solving strategy. Given a specific problem to
solve, the input to the GA is a set of potential solutions
to that problem, encoded in some fashion, and a metric
called a fitness function that allows each candidate
to be quantitatively evaluated. These candidates may be
solutions already known to work, with the aim of the GA
being to improve them, but more often they are generated at
random.
The GA then evaluates each candidate according to the
fitness function. In a pool of randomly generated
candidates, of course, most will not work at all, and these
will be deleted. However, purely by chance, a few may hold
promise - they may show activity, even if only weak and
imperfect activity, toward solving the problem.
These promising candidates are kept and allowed to
reproduce. Multiple copies are made of them, but the copies
are not perfect; random changes are introduced during the
copying process. These digital offspring then go on to the
next generation, forming a new pool of candidate solutions,
and are subjected to a second round of fitness evaluation.
Those candidate solutions which were worsened, or made no
better, by the changes to their code are again deleted; but
again, purely by chance, the random variations introduced
into the population may have improved some individuals,
making them into better, more complete or more efficient
solutions to the problem at hand. Again these winning
individuals are selected and copied over into the next
generation with random changes, and the process repeats.
The expectation is that the average fitness of the
population will increase each round, and so by repeating
this process for hundreds or thousands of rounds, very good
solutions to the problem can be discovered.
As astonishing and counterintuitive as it may seem to
some, genetic algorithms have proven to be an enormously
powerful and successful problem-solving strategy,
dramatically demonstrating the power of evolutionary
principles. Genetic algorithms have been used in a wide
variety of fields to evolve solutions to problems as
difficult as or more difficult than those faced by human
designers. Moreover, the solutions they come up with are
often more efficient, more elegant, or more complex than
anything comparable a human engineer would produce. In some
cases, genetic algorithms have come up with solutions that
baffle the programmers who wrote the algorithms in the
first place!
Methods of representation
Before a genetic algorithm can be put to work on any
problem, a method is needed to encode potential solutions
to that problem in a form that a computer can process. One
common approach is to encode solutions as binary strings:
sequences of 1's and 0's, where the digit at each position
represents the value of some aspect of the solution.
Another, similar approach is to encode solutions as arrays
of integers or decimal numbers, with each position again
representing some particular aspect of the solution. This
approach allows for greater precision and complexity than
the comparatively restricted method of using binary numbers
only and often "is intuitively closer to the problem space"
(Fleming and Purshouse 2002, p.
1228).
This technique was used, for example, in the work of
Steffen Schulze-Kremer, who wrote a genetic algorithm to
predict the three-dimensional structure of a protein based
on the sequence of amino acids that go into it (Mitchell 1996, p. 62).
Schulze-Kremer's GA used real-valued numbers to represent
the so-called "torsion angles" between the peptide bonds
that connect amino acids. (A protein is made up of a
sequence of basic building blocks called amino acids, which
are joined together like the links in a chain. Once all the
amino acids are linked, the protein folds up into a complex
three-dimensional shape based on which amino acids attract
each other and which ones repel each other. The shape of a
protein determines its function.) Genetic algorithms for
training neural networks
often use this method of encoding also.
A third approach is to represent individuals in a GA as
strings of letters, where each letter again stands for a
specific aspect of the solution. One example of this
technique is Hiroaki Kitano's "grammatical encoding"
approach, where a GA was put to the task of evolving a
simple set of rules called a context-free grammar that was
in turn used to generate neural networks for a variety of
problems (Mitchell 1996, p.
74).
The virtue of all three of these methods is that they
make it easy to define operators that cause the random
changes in the selected candidates: flip a 0 to a 1 or vice
versa, add or subtract from the value of a number by a
randomly chosen amount, or change one letter to another.
(See the section on Methods of
change for more detail about the genetic operators.)
Another strategy, developed principally by John Koza of
Stanford University and called genetic programming,
represents programs as branching data structures called
trees (Koza et al. 2003, p. 35). In
this approach, random changes can be brought about by
changing the operator or altering the value at a given node
in the tree, or replacing one subtree with another.
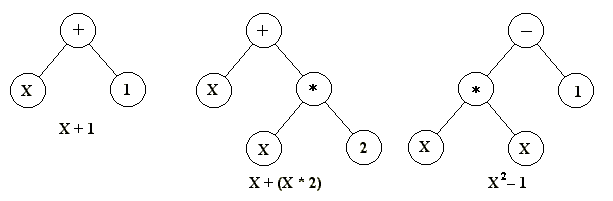
Figure 1: Three simple program
trees of the kind normally used in genetic programming. The
mathematical expression that each one represents is given
underneath.
It is important to note that evolutionary algorithms do
not need to represent candidate solutions as data strings
of fixed length. Some do represent them in this way, but
others do not; for example, Kitano's grammatical encoding
discussed above can be efficiently scaled to create large
and complex neural networks, and Koza's genetic programming
trees can grow arbitrarily large as necessary to solve
whatever problem they are applied to.
Methods of selection
There are many different techniques which a genetic
algorithm can use to select the individuals to be copied
over into the next generation, but listed below are some of
the most common methods. Some of these methods are mutually
exclusive, but others can be and often are used in
combination.
Elitist selection: The most fit members of each
generation are guaranteed to be selected. (Most GAs do not
use pure elitism, but instead use a modified form where the
single best, or a few of the best, individuals from each
generation are copied into the next generation just in case
nothing better turns up.)
Fitness-proportionate selection: More fit
individuals are more likely, but not certain, to be
selected.
Roulette-wheel selection: A form of
fitness-proportionate selection in which the chance of an
individual's being selected is proportional to the amount
by which its fitness is greater or less than its
competitors' fitness. (Conceptually, this can be
represented as a game of roulette - each individual gets a
slice of the wheel, but more fit ones get larger slices
than less fit ones. The wheel is then spun, and whichever
individual "owns" the section on which it lands each time
is chosen.)
Scaling selection: As the average fitness of the
population increases, the strength of the selective
pressure also increases and the fitness function becomes
more discriminating. This method can be helpful in making
the best selection later on when all individuals have
relatively high fitness and only small differences in
fitness distinguish one from another.
Tournament selection: Subgroups of individuals
are chosen from the larger population, and members of each
subgroup compete against each other. Only one individual
from each subgroup is chosen to reproduce.
Rank selection: Each individual in the population
is assigned a numerical rank based on fitness, and
selection is based on this ranking rather than absolute
differences in fitness. The advantage of this method is
that it can prevent very fit individuals from gaining
dominance early at the expense of less fit ones, which
would reduce the population's genetic diversity and might
hinder attempts to find an acceptable solution.
Generational selection: The offspring of the
individuals selected from each generation become the entire
next generation. No individuals are retained between
generations.
Steady-state selection: The offspring of the
individuals selected from each generation go back into the
pre-existing gene pool, replacing some of the less fit
members of the previous generation. Some individuals are
retained between generations.
Hierarchical selection: Individuals go through
multiple rounds of selection each generation. Lower-level
evaluations are faster and less discriminating, while those
that survive to higher levels are evaluated more
rigorously. The advantage of this method is that it reduces
overall computation time by using faster, less selective
evaluation to weed out the majority of individuals that
show little or no promise, and only subjecting those who
survive this initial test to more rigorous and more
computationally expensive fitness evaluation.
Methods of change
Once selection has chosen fit individuals, they must be
randomly altered in hopes of improving their fitness for
the next generation. There are two basic strategies to
accomplish this. The first and simplest is called
mutation. Just as mutation in living things changes
one gene to another, so mutation in a genetic algorithm
causes small alterations at single points in an
individual's code.
The second method is called crossover, and
entails choosing two individuals to swap segments of their
code, producing artificial "offspring" that are
combinations of their parents. This process is intended to
simulate the analogous process of recombination that occurs
to chromosomes during sexual reproduction. Common forms of
crossover include single-point crossover, in which a
point of exchange is set at a random location in the two
individuals' genomes, and one individual contributes all
its code from before that point and the other contributes
all its code from after that point to produce an offspring,
and uniform crossover, in which the value at any
given location in the offspring's genome is either the
value of one parent's genome at that location or the value
of the other parent's genome at that location, chosen with
50/50 probability.
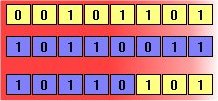
Figure 2: Crossover and mutation.
The above diagrams illustrate the effect of each of these
genetic operators on individuals in a population of 8-bit
strings. The upper diagram shows two individuals undergoing
single-point crossover; the point of exchange is set
between the fifth and sixth positions in the genome,
producing a new individual that is a hybrid of its
progenitors. The second diagram shows an individual
undergoing mutation at position 4, changing the 0 at that
position in its genome to a 1.
Other problem-solving techniques
With the rise of artificial life computing and the
development of heuristic methods, other computerized
problem-solving techniques have emerged that are in some
ways similar to genetic algorithms. This section explains
some of these techniques, in what ways they resemble GAs
and in what ways they differ.
- Neural networks
A neural network, or neural net for short, is a
problem-solving method based on a computer model of how
neurons are connected in the brain. A neural network
consists of layers of processing units called nodes joined
by directional links: one input layer, one output layer,
and zero or more hidden layers in between. An initial
pattern of input is presented to the input layer of the
neural network, and nodes that are stimulated then transmit
a signal to the nodes of the next layer to which they are
connected. If the sum of all the inputs entering one of
these virtual neurons is higher than that neuron's
so-called activation threshold, that neuron itself
activates, and passes on its own signal to neurons in the
next layer. The pattern of activation therefore spreads
forward until it reaches the output layer and is there
returned as a solution to the presented input. Just as in
the nervous system of biological organisms, neural networks
learn and fine-tune their performance over time via
repeated rounds of adjusting their thresholds until the
actual output matches the desired output for any given
input. This process can be supervised by a human
experimenter or may run automatically using a learning
algorithm (Mitchell 1996, p.
52). Genetic algorithms have been used both to build and to
train neural networks.
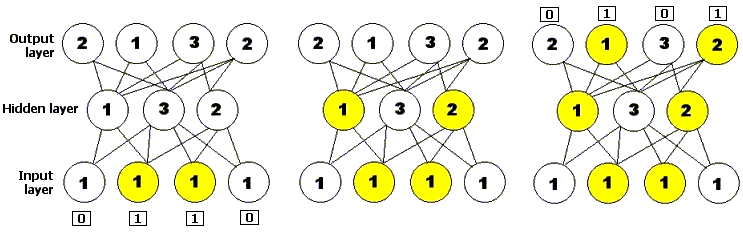
Figure 3: A simple feedforward neural network, with
one input layer consisting of four neurons, one hidden
layer consisting of three neurons, and one output layer
consisting of four neurons. The number on each neuron
represents its activation threshold: it will only fire if
it receives at least that many inputs. The diagram shows
the neural network being presented with an input string and
shows how activation spreads forward through the network to
produce an output.
- Hill-climbing
Similar to genetic algorithms, though more systematic and
less random, a hill-climbing algorithm begins with one
initial solution to the problem at hand, usually chosen at
random. The string is then mutated, and if the mutation
results in higher fitness for the new solution than for the
previous one, the new solution is kept; otherwise, the
current solution is retained. The algorithm is then
repeated until no mutation can be found that causes an
increase in the current solution's fitness, and this
solution is returned as the result (Koza et al. 2003, p. 59). (To
understand where the name of this technique comes from,
imagine that the space of all possible solutions to a given
problem is represented as a three-dimensional contour
landscape. A given set of coordinates on that landscape
represents one particular solution. Those solutions that
are better are higher in altitude, forming hills and peaks;
those that are worse are lower in altitude, forming
valleys. A "hill-climber" is then an algorithm that starts
out at a given point on the landscape and moves inexorably
uphill.) Hill-climbing is what is known as a greedy
algorithm, meaning it always makes the best choice
available at each step in the hope that the overall best
result can be achieved this way. By contrast, methods such
as genetic algorithms and simulated annealing, discussed
below, are not greedy; these methods sometimes make
suboptimal choices in the hopes that they will lead
to better solutions later on.
- Simulated annealing
Another optimization technique similar to evolutionary
algorithms is known as simulated annealing. The idea
borrows its name from the industrial process of
annealing in which a material is heated to above a
critical point to soften it, then gradually cooled in order to erase
defects in its crystalline structure, producing a more
stable and regular lattice arrangement of atoms (Haupt and Haupt 1998, p. 16). In
simulated annealing, as in genetic algorithms, there is a
fitness function that defines a fitness landscape; however,
rather than a population of candidates as in GAs, there is
only one candidate solution. Simulated annealing also adds
the concept of "temperature", a global numerical quantity
which gradually decreases over time. At each step of the
algorithm, the solution mutates (which is equivalent to
moving to an adjacent point of the fitness landscape). The
fitness of the new solution is then compared to the fitness
of the previous solution; if it is higher, the new solution
is kept. Otherwise, the algorithm makes a decision whether
to keep or discard it based on temperature. If the
temperature is high, as it is initially, even changes that
cause significant decreases in fitness may be kept and used
as the basis for the next round of the algorithm, but as
temperature decreases, the algorithm becomes more and more
inclined to only accept fitness-increasing changes.
Finally, the temperature reaches zero and the system
"freezes"; whatever configuration it is in at that point
becomes the solution. Simulated annealing is often used for
engineering design applications such as determining the
physical layout of components on a computer chip (Kirkpatrick, Gelatt and Vecchi
1983).
The earliest instances of what might today be called
genetic algorithms appeared in the late 1950s and early
1960s, programmed on computers by evolutionary biologists
who were explicitly seeking to model aspects of natural
evolution. It did not occur to any of them that this
strategy might be more generally applicable to artificial
problems, but that recognition was not long in coming:
"Evolutionary computation was definitely in the air in the
formative days of the electronic computer" (Mitchell 1996, p.2). By 1962,
researchers such as G.E.P. Box, G.J. Friedman, W.W. Bledsoe
and H.J. Bremermann had all independently developed
evolution-inspired algorithms for function optimization and
machine learning, but their work attracted little followup.
A more successful development in this area came in 1965,
when Ingo Rechenberg, then of the Technical University of
Berlin, introduced a technique he called evolution
strategy, though it was more similar to hill-climbers
than to genetic algorithms. In this technique, there was no
population or crossover; one parent was mutated to produce
one offspring, and the better of the two was kept and
became the parent for the next round of mutation (Haupt and Haupt 1998, p.146). Later
versions introduced the idea of a population. Evolution
strategies are still employed today by engineers and
scientists, especially in Germany.
The next important development in the field came in
1966, when L.J. Fogel, A.J. Owens and M.J. Walsh introduced
in America a technique they called evolutionary
programming. In this method, candidate solutions to
problems were represented as simple finite-state machines;
like Rechenberg's evolution strategy, their algorithm
worked by randomly mutating one of these simulated machines
and keeping the better of the two (Mitchell 1996, p.2; Goldberg 1989, p.105). Also like
evolution strategies, a broader formulation of the
evolutionary programming technique is still an area of
ongoing research today. However, what was still lacking in
both these methodologies was recognition of the importance
of crossover.
As early as 1962, John Holland's work on adaptive
systems laid the foundation for later developments; most
notably, Holland was also the first to explicitly propose
crossover and other recombination operators. However, the
seminal work in the field of genetic algorithms came in
1975, with the publication of the book Adaptation in
Natural and Artificial Systems. Building on earlier
research and papers both by Holland himself and by
colleagues at the University of Michigan, this book was the
first to systematically and rigorously present the concept
of adaptive digital systems using mutation, selection and
crossover, simulating processes of biological evolution, as
a problem-solving strategy. The book also attempted to put
genetic algorithms on a firm theoretical footing by
introducing the notion of schemata (Mitchell 1996, p.3; Haupt and Haupt 1998, p.147). That
same year, Kenneth De Jong's important dissertation
established the potential of GAs by showing that they could
perform well on a wide variety of test functions, including
noisy, discontinuous, and multimodal search landscapes (Goldberg 1989, p.107).
These foundational works established more widespread
interest in evolutionary computation. By the early to
mid-1980s, genetic algorithms were being applied to a broad
range of subjects, from abstract mathematical problems like
bin-packing and graph coloring to tangible engineering
issues such as pipeline flow control, pattern recognition
and classification, and structural optimization (Goldberg 1989, p. 128).
At first, these applications were mainly theoretical.
However, as research continued to proliferate, genetic
algorithms migrated into the commercial sector, their rise
fueled by the exponential growth of computing power and the
development of the Internet. Today, evolutionary
computation is a thriving field, and genetic algorithms are
"solving problems of everyday interest" (Haupt and Haupt 1998, p.147) in areas
of study as diverse as stock market prediction and
portfolio planning, aerospace engineering, microchip
design, biochemistry and molecular biology, and scheduling
at airports and assembly lines. The power of evolution has
touched virtually any field one cares to name, shaping the
world around us invisibly in countless ways, and new uses
continue to be discovered as research is ongoing. And at
the heart of it all lies nothing more than Charles Darwin's
simple, powerful insight: that the random chance of
variation, coupled with the law of selection, is a
problem-solving technique of immense power and nearly
unlimited application.
What are the strengths of GAs?
|
|
- The first and most important
point is that genetic algorithms are intrinsically
parallel. Most other algorithms are serial and can only
explore the solution space to a problem in one direction at
a time, and if the solution they discover turns out to be
suboptimal, there is nothing to do but abandon all work
previously completed and start over. However, since GAs
have multiple offspring, they can explore the solution
space in multiple directions at once. If one path turns out
to be a dead end, they can easily eliminate it and continue
work on more promising avenues, giving them a greater
chance each run of finding the optimal solution.
However, the advantage of parallelism goes beyond this.
Consider the following: All the 8-digit binary strings
(strings of 0's and 1's) form a search space, which can be
represented as ******** (where the * stands for "either 0
or 1"). The string 01101010 is one member of this space.
However, it is also a member of the space 0*******,
the space 01******, the space 0******0, the space 0*1*1*1*,
the space 01*01**0, and so on. By evaluating the fitness of
this one particular string, a genetic algorithm would be
sampling each of these many spaces to which it belongs.
Over many such evaluations, it would build up an
increasingly accurate value for the average fitness
of each of these spaces, each of which has many members.
Therefore, a GA that explicitly evaluates a small number of
individuals is implicitly evaluating a much larger group of
individuals - just as a pollster who asks questions of a
certain member of an ethnic, religious or social group
hopes to learn something about the opinions of all members
of that group, and therefore can reliably predict national
opinion while sampling only a small percentage of the
population. In the same way, the GA can "home in" on the
space with the highest-fitness individuals and find the
overall best one from that group. In the context of
evolutionary algorithms, this is known as the Schema
Theorem, and is the "central advantage" of a GA over other
problem-solving methods (Holland
1992, p. 68; Mitchell 1996,
p.28-29; Goldberg 1989,
p.20).
- Due to the parallelism that
allows them to implicitly evaluate many schema at once,
genetic algorithms are particularly well-suited to solving
problems where the space of all potential solutions is
truly huge - too vast to search exhaustively in any
reasonable amount of time. Most problems that fall into
this category are known as "nonlinear". In a linear
problem, the fitness of each component is independent, so
any improvement to any one part will result in an
improvement of the system as a whole. Needless to say, few
real-world problems are like this. Nonlinearity is the
norm, where changing one component may have ripple effects
on the entire system, and where multiple changes that
individually are detrimental may lead to much greater
improvements in fitness when combined. Nonlinearity results
in a combinatorial explosion: the space of 1,000-digit
binary strings can be exhaustively searched by evaluating
only 2,000 possibilities if the problem is linear, whereas
if it is nonlinear, an exhaustive search requires
evaluating 21000 possibilities -
a number that would take over 300 digits to write out in
full.
Fortunately, the implicit parallelism of a GA allows it to
surmount even this enormous number of possibilities,
successfully finding optimal or very good results in a
short period of time after directly sampling only small
regions of the vast fitness landscape (Forrest 1993, p. 877). For example,
a genetic algorithm developed jointly by engineers from
General Electric and Rensselaer Polytechnic Institute
produced a high-performance jet engine turbine design that
was three times better than a human-designed configuration
and 50% better than a configuration designed by an expert
system by successfully navigating a solution space
containing more than 10387
possibilities. Conventional methods for designing such
turbines are a central part of engineering projects that
can take up to five years and cost over $2 billion; the
genetic algorithm discovered this solution after two days
on a typical engineering desktop workstation (Holland 1992, p.72).
- Another notable strength of
genetic algorithms is that they perform well in problems
for which the fitness landscape is complex - ones where the
fitness function is discontinuous, noisy, changes over
time, or has many local optima. Most practical problems
have a vast solution space, impossible to search
exhaustively; the challenge then becomes how to avoid the
local optima - solutions that are better than all the
others that are similar to them, but that are not as good
as different ones elsewhere in the solution space. Many
search algorithms can become trapped by local optima: if
they reach the top of a hill on the fitness landscape, they
will discover that no better solutions exist nearby and
conclude that they have reached the best one, even though
higher peaks exist elsewhere on the map.
Evolutionary algorithms, on the other hand, have proven to
be effective at escaping local optima and discovering the
global optimum in even a very rugged and complex fitness
landscape. (It should be noted that, in reality, there is
usually no way to tell whether a given solution to a
problem is the one global optimum or just a very high local
optimum. However, even if a GA does not always deliver a
provably perfect solution to a problem, it can almost
always deliver at least a very good solution.) All four of
a GA's major components - parallelism, selection, mutation,
and crossover - work together to accomplish this. In the
beginning, the GA generates a diverse initial population,
casting a "net" over the fitness landscape. (Koza (2003, p. 506) compares this to an army
of parachutists dropping onto the landscape of a problem's
search space, with each one being given orders to find the
highest peak.) Small mutations enable each individual to
explore its immediate neighborhood, while selection focuses
progress, guiding the algorithm's offspring uphill to more
promising parts of the solution space (Holland 1992, p. 68).
However, crossover is the key element that distinguishes
genetic algorithms from other methods such as hill-climbers
and simulated annealing. Without crossover, each individual
solution is on its own, exploring the search space in its
immediate vicinity without reference to what other
individuals may have discovered. However, with crossover in
place, there is a transfer of information between
successful candidates - individuals can benefit from what
others have learned, and schemata can be mixed and
combined, with the potential to produce an offspring that
has the strengths of both its parents and the weaknesses of
neither. This point is illustrated in Koza et al. 1999, p.486, where the
authors discuss a problem of synthesizing a lowpass filter
using genetic programming. In one generation, two parent
circuits were selected to undergo crossover; one parent had
good topology (components such as inductors and capacitors
in the right places) but bad sizing (values of inductance
and capacitance for its components that were far too low).
The other parent had bad topology, but good sizing. The
result of mating the two through crossover was an offspring
with the good topology of one parent and the good sizing of
the other, resulting in a substantial improvement in
fitness over both its parents.
The problem of finding the global optimum in a space with
many local optima is also known as the dilemma of
exploration vs. exploitation, "a classic problem for all
systems that can adapt and learn" (Holland 1992, p. 69). Once an
algorithm (or a human designer) has found a problem-solving
strategy that seems to work satisfactorily, should it
concentrate on making the best use of that strategy, or
should it search for others? Abandoning a proven strategy
to look for new ones is almost guaranteed to involve losses
and degradation of performance, at least in the short term.
But if one sticks with a particular strategy to the
exclusion of all others, one runs the risk of not
discovering better strategies that exist but have not yet
been found. Again, genetic algorithms have shown themselves
to be very good at striking this balance and discovering
good solutions with a reasonable amount of time and
computational effort.
- Another area in which
genetic algorithms excel is their ability to manipulate
many parameters simultaneously (Forrest 1993, p. 874). Many
real-world problems cannot be stated in terms of a single
value to be minimized or maximized, but must be expressed
in terms of multiple objectives, usually with tradeoffs
involved: one can only be improved at the expense of
another. GAs are very good at solving such problems: in
particular, their use of parallelism enables them to
produce multiple equally good solutions to the same
problem, possibly with one candidate solution optimizing
one parameter and another candidate optimizing a different
one (Haupt and Haupt 1998, p.17),
and a human overseer can then select one of these
candidates to use. If a particular solution to a
multiobjective problem optimizes one parameter to a degree
such that that parameter cannot be further improved without
causing a corresponding decrease in the quality of some
other parameter, that solution is called Pareto
optimal or non-dominated (Coello 2000, p. 112).
- Finally, one of the
qualities of genetic algorithms which might at first appear
to be a liability turns out to be one of their strengths:
namely, GAs know nothing about the problems they are
deployed to solve. Instead of using previously known
domain-specific information to guide each step and making
changes with a specific eye towards improvement, as human
designers do, they are "blind watchmakers" (Dawkins 1996); they make
random changes to their candidate solutions and then
use the fitness function to determine whether those changes
produce an improvement.
The virtue of this technique is that it allows genetic
algorithms to start out with an open mind, so to speak.
Since its decisions are based on randomness, all
possible search pathways are theoretically open to a GA; by
contrast, any problem-solving strategy that relies on prior
knowledge must inevitably begin by ruling out many pathways
a priori, therefore missing any novel solutions that
may exist there (Koza et al. 1999,
p. 547). Lacking preconceptions based on established
beliefs of "how things should be done" or what "couldn't
possibly work", GAs do not have this problem. Similarly,
any technique that relies on prior knowledge will break
down when such knowledge is not available, but again, GAs
are not adversely affected by ignorance (Goldberg 1989, p. 23). Through
their components of parallelism, crossover and mutation,
they can range widely over the fitness landscape, exploring
regions which intelligently produced algorithms might have
overlooked, and potentially uncovering solutions of
startling and unexpected creativity that might never have
occurred to human designers. One vivid illustration of this
is the rediscovery, by genetic programming, of the concept
of negative feedback - a principle crucial to many
important electronic components today, but one that, when
it was first discovered, was denied a patent for nine years
because the concept was so contrary to established beliefs
(Koza et al. 2003, p. 413).
Evolutionary algorithms, of course, are neither aware nor
concerned whether a solution runs counter to established
beliefs - only whether it works.
What are the limitations of GAs?
|
|
Although genetic algorithms have proven to be an
efficient and powerful problem-solving strategy, they are
not a panacea. GAs do have certain limitations; however, it
will be shown that all of these can be overcome and none of
them bear on the validity of biological evolution.
- The first, and most
important, consideration in creating a genetic algorithm is
defining a representation for the problem. The language
used to specify candidate solutions must be robust; i.e.,
it must be able to tolerate random changes such that fatal
errors or nonsense do not consistently result.
There are two main ways of achieving this. The first, which
is used by most genetic algorithms, is to define
individuals as lists of numbers - binary-valued,
integer-valued, or real-valued - where each number
represents some aspect of a candidate solution. If the
individuals are binary strings, 0 or 1 could stand for the
absence or presence of a given feature. If they are lists
of numbers, these numbers could represent many different
things: the weights of the links in a neural network, the
order of the cities visited in a given tour, the spatial
placement of electronic components, the values fed into a
controller, the torsion angles of peptide bonds in a
protein, and so on. Mutation then entails changing these
numbers, flipping bits or adding or subtracting random
values. In this case, the actual program code does not
change; the code is what manages the simulation and keeps
track of the individuals, evaluating their fitness and
perhaps ensuring that only values realistic and possible
for the given problem result.
In another method, genetic programming, the actual program
code does change. As discussed in the section Methods of representation,
GP represents individuals as executable trees of code that
can be mutated by changing or swapping subtrees. Both of
these methods produce representations that are robust
against mutation and can represent many different kinds of
problems, and as discussed in the section Some specific examples, both have had
considerable success.
This issue of representing candidate solutions in a robust
way does not arise in nature, because the method of
representation used by evolution, namely the genetic code,
is inherently robust: with only a very few exceptions, such
as a string of stop codons, there is no such thing as a
sequence of DNA bases that cannot be translated into a
protein. Therefore, virtually any change to an individual's
genes will still produce an intelligible result, and so
mutations in evolution have a higher chance of producing an
improvement. This is in contrast to human-created languages
such as English, where the number of meaningful words is
small compared to the total number of ways one can combine
letters of the alphabet, and therefore random changes to an
English sentence are likely to produce nonsense.
- The problem of how to write
the fitness function must be carefully considered so that
higher fitness is attainable and actually does equate to a
better solution for the given problem. If the fitness
function is chosen poorly or defined imprecisely, the
genetic algorithm may be unable to find a solution to the
problem, or may end up solving the wrong problem. (This
latter situation is sometimes described as the tendency of
a GA to "cheat", although in reality all that is happening
is that the GA is doing what it was told to do, not what
its creators intended it to do.) An example of this can be
found in Graham-Rowe 2002, in
which researchers used an evolutionary algorithm in
conjunction with a reprogrammable hardware array, setting
up the fitness function to reward the evolving circuit for
outputting an oscillating signal. At the end of the
experiment, an oscillating signal was indeed being produced
- but instead of the circuit itself acting as an
oscillator, as the researchers had intended, they
discovered that it had become a radio receiver that was
picking up and relaying an oscillating signal from a nearby
piece of electronic equipment!
This is not a problem in nature, however. In the laboratory
of biological evolution there is only one fitness function,
which is the same for all living things - the drive to
survive and reproduce, no matter what adaptations make this
possible. Those organisms which reproduce more abundantly
compared to their competitors are more fit; those which
fail to reproduce are unfit.
- In addition to making a
good choice of fitness function, the other parameters of a
GA - the size of the population, the rate of mutation and
crossover, the type and strength of selection - must be
also chosen with care. If the population size is too small,
the genetic algorithm may not explore enough of the
solution space to consistently find good solutions. If the
rate of genetic change is too high or the selection scheme
is chosen poorly, beneficial schema may be disrupted and
the population may enter error catastrophe, changing too
fast for selection to ever bring about convergence.
Living things do face similar difficulties, and
evolution has dealt with them. It is true that if a
population size falls too low, mutation rates are too high,
or the selection pressure is too strong (such a situation
might be caused by drastic environmental change), then the
species may go extinct. The solution has been "the
evolution of evolvability" - adaptations that alter a
species' ability to adapt. For example, most living things
have evolved elaborate molecular machinery that checks for
and corrects errors during the process of DNA replication,
keeping their mutation rate down to acceptably low levels;
conversely, in times of severe environmental stress, some
bacterial species enter a state of hypermutation
where the rate of DNA replication errors rises sharply,
increasing the chance that a compensating mutation will be
discovered. Of course, not all catastrophes can be evaded,
but the enormous diversity and highly complex adaptations
of living things today show that, in general, evolution is
a successful strategy. Likewise, the diverse applications
of and impressive results produced by genetic algorithms
show them to be a powerful and worthwhile field of
study.
- One type of problem that
genetic algorithms have difficulty dealing with are
problems with "deceptive" fitness functions (Mitchell 1996, p.125), those where
the locations of improved points give misleading
information about where the global optimum is likely to be
found. For example, imagine a problem where the search
space consisted of all eight-character binary strings, and
the fitness of an individual was directly proportional to
the number of 1s in it - i.e., 00000001 would be less fit
than 00000011, which would be less fit than 00000111, and
so on - with two exceptions: the string 11111111 turned out
to have very low fitness, and the string 00000000 turned
out to have very high fitness. In such a problem, a GA (as
well as most other algorithms) would be no more likely to
find the global optimum than random search.
The resolution to this problem is the same for both genetic
algorithms and biological evolution: evolution is not a
process that has to find the single global optimum every
time. It can do almost as well by reaching the top of a
high local optimum, and for most situations, this will
suffice, even if the global optimum cannot easily be
reached from that point. Evolution is very much a
"satisficer" - an algorithm that delivers a "good enough"
solution, though not necessarily the best possible
solution, given a reasonable amount of time and effort
invested in the search. The Evidence for Jury-Rigged
Design in Nature FAQ gives examples of this very
outcome appearing in nature. (It is also worth noting that
few, if any, real-world problems are as fully deceptive as
the somewhat contrived example given above. Usually, the
location of local improvements gives at least some
information about the location of the global
optimum.)
- One well-known problem
that can occur with a GA is known as premature
convergence. If an individual that is more fit than
most of its competitors emerges early on in the course of
the run, it may reproduce so abundantly that it drives down
the population's diversity too soon, leading the algorithm
to converge on the local optimum that that individual
represents rather than searching the fitness landscape
thoroughly enough to find the global optimum (Forrest 1993, p. 876; Mitchell 1996, p. 167). This is an
especially common problem in small populations, where even
chance variations in reproduction rate may cause one
genotype to become dominant over others.
The most common methods implemented by GA researchers to
deal with this problem all involve controlling the strength
of selection, so as not to give excessively fit individuals
too great of an advantage. Rank,
scaling and tournament selection, discussed earlier,
are three major means for accomplishing this; some methods
of scaling selection include sigma scaling, in which
reproduction is based on a statistical comparison to the
population's average fitness, and Boltzmann selection, in
which the strength of selection increases over the course
of a run in a manner similar to the "temperature" variable
in simulated annealing (Mitchell
1996, p. 168).
Premature convergence does occur in nature (where it
is called genetic
drift by biologists). This should not be surprising; as
discussed above, evolution as a problem-solving strategy is
under no obligation to find the single best solution,
merely one that is good enough. However, premature
convergence in nature is less common since most beneficial
mutations in living things produce only small, incremental
fitness improvements; mutations that produce such a large
fitness gain as to give their possessors dramatic
reproductive advantage are rare.
- Finally, several
researchers (Holland 1992, p.72;
Forrest 1993, p.875; Haupt and Haupt 1998, p.18) advise
against using genetic algorithms on analytically solvable
problems. It is not that genetic algorithms cannot find
good solutions to such problems; it is merely that
traditional analytic methods take much less time and
computational effort than GAs and, unlike GAs, are usually
mathematically guaranteed to deliver the one exact
solution. Of course, since there is no such thing as a
mathematically perfect solution to any problem of
biological adaptation, this issue does not arise in
nature.
Some specific examples of GAs
|
|
As the power of evolution gains increasingly widespread
recognition, genetic algorithms have been used to tackle a
broad variety of problems in an extremely diverse array of
fields, clearly showing their power and their potential.
This section will discuss some of the more noteworthy uses
to which they have been put.
- Acoustics
Sato et al. 2002 used genetic
algorithms to design a concert hall with optimal acoustic
properties, maximizing the sound quality for the audience,
for the conductor, and for the musicians on stage. This
task involves the simultaneous optimization of multiple
variables. Beginning with a shoebox-shaped hall, the
authors' GA produced two non-dominated solutions, both of
which were described as "leaf-shaped" (p.526). The authors
state that these solutions have proportions similar to
Vienna's Grosser Musikvereinsaal, which is widely agreed to
be one of the best - if not the best - concert hall in the
world in terms of acoustic properties.
Porto, Fogel and Fogel 1995 used
evolutionary programming to train neural networks to
distinguish between sonar reflections from different types
of objects: man-made metal spheres, sea mounts, fish and
plant life, and random background noise. After 500
generations, the best evolved neural network had a
probability of correct classification ranging between 94%
and 98% and a probability of misclassification between 7.4%
and 1.5%, which are "reasonable probabilities of detection
and false alarm" (p.21). The evolved network matched the
performance of another network developed by simulated
annealing and consistently outperformed networks trained by
back propagation, which "repeatedly stalled at suboptimal
weight sets that did not yield satisfactory results"
(p.21). By contrast, both stochastic methods showed
themselves able to overcome these local optima and produce
smaller, effective and more robust networks; but the
authors suggest that the evolutionary algorithm, unlike
simulated annealing, operates on a population and so takes
advantage of global information about the search space,
potentially leading to better performance in the long
run.
Tang et al. 1996 survey the uses of
genetic algorithms within the field of acoustics and signal
processing. One area of particular interest involves the
use of GAs to design Active Noise Control (ANC) systems,
which cancel out undesired sound by producing sound waves
that destructively interfere with the unwanted noise. This
is a multiple-objective problem requiring the precise
placement and control of multiple loudspeakers; GAs have
been used both to design the controllers and find the
optimal placement of the loudspeakers for such systems,
resulting in the "effective attenuation of noise" (p.33) in
experimental tests.
- Aerospace
engineering
Obayashi et al. 2000 used a
multiple-objective genetic algorithm to design the wing
shape for a supersonic aircraft. Three major considerations
govern the wing's configuration - minimizing aerodynamic
drag at supersonic cruising speeds, minimizing drag at
subsonic speeds, and minimizing aerodynamic load (the
bending force on the wing). These objectives are mutually
exclusive, and optimizing them all simultaneously requires
tradeoffs to be made.
The chromosome in this problem is a string of 66
real-valued numbers, each of which corresponds to a
specific aspect of the wing: its shape, its thickness, its
twist, and so on. Evolution with elitist rank selection was
simulated for 70 generations, with a population size of 64
individuals. At the termination of this process, there were
several Pareto-optimal individuals, each one representing a
single non-dominated solution to the problem. The paper
notes that these best-of-run individuals have "physically
reasonable" characteristics, indicating the validity of the
optimization technique (p.186). To further evaluate the
quality of the solutions, six of the best were compared to
a supersonic wing design produced by the SST Design Team of
Japan's National Aerospace Laboratory. All six were
competitive, having drag and load values approximately
equal to or less than the human-designed wing; one of the
evolved solutions in particular outperformed the NAL's
design in all three objectives. The authors note that the
GA's solutions are similar to a design called the "arrow
wing" which was first suggested in the late 1950s, but
ultimately abandoned in favor of the more conventional
delta-wing design.
In a follow-up paper (Sasaki et al.
2001), the authors repeat their experiment while adding
a fourth objective, namely minimizing the twisting
moment of the wing (a known potential problem for
arrow-wing SST designs). Additional control points for
thickness are also added to the array of design variables.
After 75 generations of evolution, two of the best
Pareto-optimal solutions were again compared to the
Japanese National Aerospace Laboratory's wing design for
the NEXST-1 experimental supersonic airplane. It was found
that both of these designs (as well as one optimal design
from the previous simulation, discussed above) were
physically reasonable and superior to the NAL's design in
all four objectives.
Williams, Crossley and Lang
2001 applied genetic algorithms to the task of spacing
satellite orbits to minimize coverage blackouts. As
telecommunications technology continues to improve, humans
are increasingly dependent on Earth-orbiting satellites to
perform many vital functions, and one of the problems
engineers face is designing their orbital trajectories.
Satellites in high Earth orbit, around 22,000 miles up, can
see large sections of the planet at once and be in constant
contact with ground stations, but these are far more
expensive to launch and more vulnerable to cosmic
radiation. It is more economical to put satellites in low
orbits, as low as a few hundred miles in some cases, but
because of the curvature of the Earth it is inevitable that
these satellites will at times lose line-of-sight access to
surface receivers and thus be useless. Even constellations
of several satellites experience unavoidable blackouts and
losses of coverage for this reason. The challenge is to
arrange the satellites' orbits to minimize this downtime.
This is a multi-objective problem, involving the
minimization of both the average blackout time for all
locations and the maximum blackout time for any one
location; in practice, these goals turn out to be mutually
exclusive.
When the GA was applied to this problem, the evolved
results for three, four and five-satellite constellations
were unusual, highly asymmetric orbit configurations, with
the satellites spaced by alternating large and small gaps
rather than equal-sized gaps as conventional techniques
would produce. However, this solution significantly reduced
both average and maximum revisit times, in some cases by up
to 90 minutes. In a news article about the results, Dr.
William Crossley noted that "engineers with years of
aerospace experience were surprised by the higher
performance offered by the unconventional design".
| Keane and Brown 1996 used a GA
to evolve a new design for a load-bearing truss or boom
that could be assembled in orbit and used for satellites,
space stations and other aerospace construction projects.
The result, a twisted, organic-looking structure that has
been compared to a human leg bone, uses no more material
than the standard truss design but is lightweight, strong
and far superior at damping out damaging vibrations, as was
confirmed by real-world tests of the final product. And yet
"No intelligence made the designs. They just evolved" (Petit 1998). The authors of the paper
further note that their GA only ran for 10 generations due
to the computationally intensive nature of the simulation,
and the population had not become stagnant. Continuing the
run for more generations would undoubtedly have produced
further improvements in performance. |
Figure 4: A genetically optimized three-dimensional
truss with improved frequency response. (Adapted from [1].) |
Finally, as reported in Gibbs
1996, Lockheed Martin has used a genetic algorithm to
evolve a series of maneuvers to shift a spacecraft from one
orientation to another within 2% of the theoretical minimum
time for such maneuvers. The evolved solution was 10%
faster than a solution hand-crafted by an expert for the
same problem.
- Astronomy and
astrophysics
Charbonneau 1995 suggests
the usefulness of GAs for problems in astrophysics by
applying them to three example problems: fitting the
rotation curve of a galaxy based on observed rotational
velocities of its components, determining the pulsation
period of a variable star based on time-series data, and
solving for the critical parameters in a
magnetohydrodynamic model of the solar wind. All three of
these are hard multi-dimensional nonlinear problems.
Charbonneau's genetic algorithm, PIKAIA, uses generational,
fitness-proportionate ranking selection coupled with
elitism, ensuring that the single best individual is copied
over once into the next generation without modification.
PIKAIA has a crossover rate of 0.65 and a variable mutation
rate that is set to 0.003 initially and gradually increases
later on, as the population approaches convergence, to
maintain variability in the gene pool.
In the galactic rotation-curve problem, the GA produced two
curves, both of which were very good fits to the data (a
common result in this type of problem, in which there is
little contrast between neighboring hilltops); further
observations can then distinguish which one is to be
preferred. In the time-series problem, the GA was
impressively successful in autonomously generating a
high-quality fit for the data, but harder problems were not
fitted as well (although, Charbonneau points out, these
problems are equally difficult to solve with conventional
techniques). The paper suggests that a hybrid GA employing
both artificial evolution and standard analytic techniques
might perform better. Finally, in solving for the six
critical parameters of the solar wind, the GA successfully
determined the value of three of them to an accuracy of
within 0.1% and the remaining three to accuracies of within
1 to 10%. (Though lower experimental error for these three
would always be preferable, Charbonneau notes that there
are no other robust, efficient methods for experimentally
solving a six-dimensional nonlinear problem of this type; a
conjugate gradient method works "as long as a very
good starting guess can be provided" (p.323). By contrast,
GAs do not require such finely tuned domain-specific
knowledge.)
Based on the results obtained so far, Charbonneau suggests
that GAs can and should find use in other difficult
problems in astrophysics, in particular inverse problems
such as Doppler imaging and helioseismic inversions. In
closing, Charbonneau argues that GAs are a "strong and
promising contender" (p.324) in this field, one that can be
expected to complement rather than replace traditional
optimization techniques, and concludes that "the bottom
line, if there is to be one, is that genetic algorithms
work, and often frightfully well" (p.325).
- Chemistry
High-powered, ultrashort pulses of laser energy can split
apart complex molecules into simpler molecules, a process
with important applications to organic chemistry and
microelectronics. The specific end products of such a
reaction can be controlled by modulating the phase of the
laser pulse. However, for large molecules, solving for the
desired pulse shape analytically is too difficult: the
calculations are too complex and the relevant
characteristics (the potential energy surfaces of the
molecules) are not known precisely enough.
Assion et al. 1998 solved this
problem by using an evolutionary algorithm to design the
pulse shape. Instead of inputting complex, problem-specific
knowledge about the quantum characteristics of the input
molecules to design the pulse to specifications, the EA
fires a pulse, measures the proportions of the resulting
product molecules, randomly mutates the beam
characteristics with the hope of getting these proportions
closer to the desired output, and the process repeats.
(Rather than fine-tune any characteristics of the laser
beam directly, the authors' GA represents individuals as a
set of 128 numbers, each of which is a voltage value that
controls the refractive index of one of the pixels in the
laser light modulator. Again, no problem-specific knowledge
about the properties of either the laser or the reaction
products is needed.) The authors state that their
algorithm, when applied to two sample substances,
"automatically finds the best configuration... no matter
how complicated the molecular response may be" (p.920),
demonstrating "automated coherent control on products that
are chemically different from each other and from the
parent molecule" (p.921).
In the early to mid-1990s, the widespread adoption of a
novel drug design technique called combinatorial
chemistry revolutionized the pharmaceutical industry.
In this method, rather than the painstaking, precise
synthesis of a single compound at a time, biochemists
deliberately mix a wide variety of reactants to produce an
even wider variety of products - hundreds, thousands or
millions of different compounds per batch - which can then
be rapidly screened for biochemical activity. In designing
libraries of reactants for this technique, there are two
main approaches: reactant-based design, which chooses
optimized groups of reactants without considering what
products will result, and product-based design, which
selects reactants most likely to produce products with the
desired properties. Product-based design is more difficult
and complex, but has been shown to result in better and
more diverse combinatorial libraries and a greater
likelihood of getting a usable result.
In a paper funded by GlaxoSmithKline's research and
development department, Gillet
2002 discusses the use of a multiobjective genetic
algorithm for the product-based design of combinatorial
libraries. In choosing the compounds that go into a
particular library, qualities such as molecular diversity
and weight, cost of supplies, toxicity, absorption,
distribution, and metabolism must all be considered. If the
aim is to find molecules similar to an existing molecule of
known function (a common method of new drug design),
structural similarity can also be taken into account. This
paper presents a multiobjective approach where a set of
Pareto-optimal results that maximize or minimize each of
these objectives can be developed. The author concludes
that the GA was able to simultaneously satisfy the criteria
of molecular diversity and maximum synthetic efficiency,
and was able to find molecules that were drug-like as well
as "very similar to given target molecules after exploring
a very small fraction of the total search space"
(p.378).
In a related paper, Glen and Payne
1995 discuss the use of genetic algorithms to
automatically design new molecules from scratch to fit a
given set of specifications. Given an initial population
either generated randomly or using the simple molecule
ethane as a seed, the GA randomly adds, removes and alters
atoms and molecular fragments with the aim of generating
molecules that fit the given constraints. The GA can
simultaneously optimize a large number of objectives,
including molecular weight, molecular volume, number of
bonds, number of chiral centers, number of atoms, number of
rotatable bonds, polarizability, dipole moment, and more in
order to produce candidate molecules with the desired
properties. Based on experimental tests, including one
difficult optimization problem that involved generating
molecules with properties similar to ribose (a sugar
compound frequently mimicked in antiviral drugs), the
authors conclude that the GA is an "excellent idea
generator" (p.199) that offers "fast and powerful
optimisation properties" and can generate "a diverse set of
possible structures" (p.182). They go on to state, "Of
particular note is the powerful optimising ability of the
genetic algorithm, even with relatively small population
sizes" (p.200). In a sign that these results are not merely
theoretical, Lemley 2001 reports
that the Unilever corporation has used genetic algorithms
to design new antimicrobial compounds for use in cleansers,
which it has patented.
- Electrical
engineering
A field-programmable gate array, or FPGA for short, is a
special type of circuit board with an array of logic cells,
each of which can act as any type of logic gate, connected
by flexible interlinks which can connect cells. Both of
these functions are controlled by software, so merely by
loading a special program into the board, it can be altered
on the fly to perform the functions of any one of a vast
variety of hardware devices.
Dr. Adrian Thompson has exploited this device, in
conjunction with the principles of evolution, to produce a
prototype voice-recognition circuit that can distinguish
between and respond to spoken commands using only 37 logic
gates - a task that would have been considered impossible
for any human engineer. He generated random bit strings of
0s and 1s and used them as configurations for the FPGA,
selecting the fittest individuals from each generation,
reproducing and randomly mutating them, swapping sections
of their code and passing them on to another round of
selection. His goal was to evolve a device that could at
first discriminate between tones of different frequencies
(1 and 10 kilohertz), then distinguish between the spoken
words "go" and "stop".
This aim was achieved within 3000 generations, but the
success was even greater than had been anticipated. The
evolved system uses far fewer cells than anything a human
engineer could have designed, and it does not even need the
most critical component of human-built systems - a clock.
How does it work? Thompson has no idea, though he has
traced the input signal through a complex arrangement of
feedback loops within the evolved circuit. In fact, out of
the 37 logic gates the final product uses, five of them are
not even connected to the rest of the circuit in any way -
yet if their power supply is removed, the circuit stops
working. It seems that evolution has exploited some subtle
electromagnetic effect of these cells to come up with its
solution, yet the exact workings of the complex and
intricate evolved structure remain a mystery (Davidson 1997).
Altshuler and Linden 1997 used
a genetic algorithm to evolve wire antennas with
pre-specified properties. The authors note that the design
of such antennas is an imprecise process, starting with the
desired properties and then determining the antenna's shape
through "guesses.... intuition, experience, approximate
equations or empirical studies" (p.50). This technique is
time-consuming, often does not produce optimal results, and
tends to work well only for relatively simple, symmetric
designs. By contrast, in the genetic algorithm approach,
the engineer specifies the antenna's electromagnetic
properties, and the GA automatically synthesizes a matching
configuration.
Figure 5: A crooked-wire genetic antenna
(after Altshuler and Linden
1997, figure 1). |
Altshuler and Linden used their GA to
design a circularly polarized seven-segment antenna with
hemispherical coverage; the result is shown to the left.
Each individual in the GA consisted of a binary chromosome
specifying the three-dimensional coordinates of each end of
each wire. Fitness was evaluated by simulating each
candidate according to an electromagnetic wiring code, and
the best-of-run individual was then built and tested. The
authors describe the shape of this antenna, which does not
resemble traditional antennas and has no obvious symmetry,
as "unusually weird" and "counter-intuitive" (p.52), yet it
had a nearly uniform radiation pattern with high bandwidth
both in simulation and in experimental testing, excellently
matching the prior specification. The authors conclude that
a genetic algorithm-based method for antenna design shows
"remarkable promise". "...this new design procedure is
capable of finding genetic antennas able to effectively
solve difficult antenna problems, and it will be
particularly useful in situations where existing designs
are not adequate" (p.52). |
- Financial
markets
Mahfoud and Mani 1996 used a
genetic algorithm to predict the future performance of 1600
publicly traded stocks. Specifically, the GA was tasked
with forecasting the relative return of each stock, defined
as that stock's return minus the average return of all 1600
stocks over the time period in question, 12 weeks (one
calendar quarter) into the future. As input, the GA was
given historical data about each stock in the form of a
list of 15 attributes, such as price-to-earnings ratio and
growth rate, measured at various past points in time; the
GA was asked to evolve a set of if/then rules to classify
each stock and to provide, as output, both a recommendation
on what to do with regards to that stock (buy, sell, or no
prediction) and a numerical forecast of the relative
return. The GA's results were compared to those of an
established neural net-based system which the authors had
been using to forecast stock prices and manage portfolios
for three years previously. Of course, the stock market is
an extremely noisy and nonlinear system, and no predictive
mechanism can be correct 100% of the time; the challenge is
to find a predictor that is accurate more often than
not.
In the experiment, the GA and the neural net each made
forecasts at the end of the week for each one of the 1600
stocks, for twelve consecutive weeks. Twelve weeks after
each prediction, the actual performance was compared with
the predicted relative return. Overall, the GA
significantly outperformed the neural network: in one trial
run, the GA correctly predicted the direction of one stock
47.6% of the time, made no prediction 45.8% of the time,
and made an incorrect prediction only 6.6% of the time, for
an overall predictive accuracy of 87.8%. Although the
neural network made definite predictions more often, it was
also wrong in its predictions more often (in fact, the
authors speculate that the GA's greater ability to make no
prediction when the data were uncertain was a factor in its
success; the neural net always produces a prediction unless
explicitly restricted by the programmer). In the 1600-stock
experiment, the GA produced a relative return of +5.47%,
versus +4.40% for the neural net - a statistically
significant difference. In fact, the GA also significantly
outperformed three major stock market indices - the S&P
500, the S&P 400, and the Russell 2000 - over this
period; chance was excluded as the cause of this result at
the 95% confidence level. The authors attribute this
compelling success to the ability of the genetic algorithm
to learn nonlinear relationships not readily apparent to
human observers, as well as the fact that it lacks a human
expert's "a priori bias against counterintuitive or
contrarian rules" (p.562).
Similar success was achieved by Andreou, Georgopoulos and Likothanassis
2002, who used hybrid genetic algorithms to evolve
neural networks that predicted the exchange rates of
foreign currencies up to one month ahead. As opposed to the
last example, where GAs and neural nets were in
competition, here the two worked in concert, with the GA
evolving the architecture (number of input units, number of
hidden units, and the arrangement of the links between
them) of the network which was then trained by a filter
algorithm.
As historical information, the algorithm was given 1300
previous raw daily values of five currencies - the American
dollar, the German deutsche mark, the French franc, the
British pound, and the Greek drachma - and asked to predict
their future values 1, 2, 5, and 20 days ahead. The hybrid
GA's performance, in general, showed a "remarkable level of
accuracy" (p.200) in all cases tested, outperforming
several other methods including neural networks alone.
Correlations for the one-day case ranged from 92 to 99%,
and though accuracy decreased over increasingly greater
time lags, the GA continued to be "quite successful"
(p.206) and clearly outperformed the other methods. The
authors conclude that "remarkable prediction success has
been achieved in both a one-step ahead and a multistep
predicting horizon" (p.208) - in fact, they state that
their results are better by far than any related predictive
strategies attempted on this data series or other
currencies.
The uses of GAs on the financial markets have begun to
spread into real-world brokerage firms. Naik 1996 reports that LBS Capital
Management, an American firm headquartered in Florida, uses
genetic algorithms to pick stocks for a pension fund it
manages. Coale 1997 and Begley and Beals 1995 report that
First Quadrant, an investment firm in California that
manages over $2.2 billion, uses GAs to make investment
decisions for all of their financial services. Their
evolved model earns, on average, $255 for every $100
invested over six years, as opposed to $205 for other types
of modeling systems.
- Game
playing
One of the most novel and compelling demonstrations of the
power of genetic algorithms was presented by Chellapilla and Fogel 2001, who
used a GA to evolve neural networks that could play the
game of checkers. The authors state that one of the major
difficulties in these sorts of strategy-related problems is
the credit assignment problem - in other words, how
does one write a fitness function? It has been widely
believed that the mere criterion of win, lose or draw does
not provide sufficient information for an evolutionary
algorithm to figure out what constitutes good play.
In this paper, Chellapilla and Fogel overturn that
assumption. Given only the spatial positions of pieces on
the checkerboard and the total number of pieces possessed
by each side, they were able to evolve a checkers program
that plays at a level competitive with human experts,
without any intelligent input as to what constitutes good
play - indeed, the individuals in the evolutionary algorithm
were not even told what the criteria for a win were, nor were
they told the result of any one game.
In Chellapilla and Fogel's representation, the game state was represented by a numeric list of 32 elements, with each position in the list corresponding to an available position on the board. The value at each position was either 0 for an unoccupied square, -1 if that
square was occupied by an enemy checker, +1 if that square
was occupied by one of the program's checkers, and -K or +K
for a square occupied by an enemy or friendly king. (The
value of K was not pre-specified, but again was determined
by evolution over the course of the algorithm.)
Accompanying this was a neural network with multiple
processing layers and one input layer with a node for each
of the possible 4x4, 5x5, 6x6, 7x7 and 8x8 squares on the
board. The output of the neural net for any given
arrangement of pieces was a value from -1 to +1 indicating
how good it felt that position was for it. For each move,
the neural network was presented with a game tree listing
all possible moves up to four turns into the future, and a
move decision was made based on which branch of the tree
produced the best results for it.
The evolutionary algorithm began with a population of 15 neural networks with randomly generated weights and biases assigned to each node and link; each individual then reproduced once, generating an offspring with variations in the values of the network. These 30 individuals then competed for survival by playing against each other, with each individual competing against 5 randomly chosen opponents per turn. 1 point was awarded for each win and 2 points were deducted for each loss. The 15 best performers, based on total score, were selected to produce offspring for the next generation, and the process repeated. Evolution was continued for 840 generations (approximately six months of computer time).
| Class |
Rating |
| Senior Master |
2400+ |
| Master |
2200-2399 |
| Expert |
2000-2199 |
| Class A |
1800-1999 |
| Class B |
1600-1799 |
| Class C |
1400-1599 |
| Class J |
< 200 |
|
The single best individual that emerged
from this selection was entered as a competitor on the
gaming website www.zone.com. Over a period
of two months, it played against 165 human opponents
comprising a range of high skill levels, from class C to
master, according to the ranking system of the United
States Chess Federation (shown at left, some ranks omitted
for clarity). Of these games, the neural net won 94, lost
39 and drew 32; based on the rankings of the opponents in
these games, the evolved neural net was equivalent to a
player with a mean rating of 2045.85, placing it at the
expert level - a higher ranking than 99.61% of over 80,000
players registered at the website. One of the neural net's
most significant victories was when it defeated a player
ranked 98th out of all registered players, whose rating was
just 27 points below master level. |
Tests conducted with a simple piece-differential program
(which bases moves solely on the difference between the number of checkers remaining to each side) with an eight-move look-ahead showed the neural net to be significantly superior, with a
rating over 400 points higher. "A program that relies only
on the piece count and an eight-ply search will defeat a
lot of people, but it is not an expert. The best evolved
neural network is" (p.425). Even when it was searching
positions two further moves ahead than the neural net, the
piece-differential program lost decisively in eight out of
ten games. This conclusively demonstrates that the evolved
neural net is not merely counting pieces, but is somehow
processing spatial characteristics of the board to decide
its moves. The authors point out that opponents on zone.com
often commented that the neural net's moves were "strange",
but its overall level of play was described as "very tough"
or with similar complimentary terms.
To further test the evolved neural network (which the
authors named "Anaconda" since it often won by restricting
its opponents' mobility), it was played against a
commercial checkers program, Hoyle's Classic Games,
distributed by Sierra Online (Chellapilla and Fogel 2000).
This program comes with a variety of built-in characters,
each of whom plays at a different skill level. Anaconda was
tested against three characters ("Beatrice", "Natasha" and
"Leopold") designated as expert-level players, playing one
game as red and one game as white against each of them with
a six-ply look-ahead. Though the authors doubted that this
depth of look-ahead would give Anaconda the ability to play
at the expert skill level it had previously shown, it won
six straight victories out of all six games played. Based
on this outcome, the authors expressed skepticism over
whether the Hoyle software played at the skill level
advertised, though it should be noted that they reached
this conclusion based solely on the ease with which
Anaconda defeated it!
The ultimate test of Anaconda was given in Chellapilla and Fogel 2002,
where the evolved neural net was matched against the best
checkers player in the world: Chinook, a
program designed principally by Dr. Jonathan Schaeffer of
the University of Alberta. Rated at 2814 in 1996 (with its
closest human competitors rated in the 2600s), Chinook
incorporates a book of opening moves provided by human
grandmasters, a sophisticated set of middle-game
algorithms, and a complete database of all possible moves
with ten pieces on the board or less, so it never makes a
mistake in the endgame. An enormous amount of human
intelligence and expertise went into the design of this
program.
Chellapilla and Fogel pitted Anaconda against Chinook in a
10-game tournament, with Chinook playing at a 5-ply skill
level, making it roughly approximate to master level.
Chinook won this contest, four wins to two with four draws.
(Interestingly, the authors note, in two of the games that
ended as draws, Anaconda held the lead with four kings to
Chinook's three. Furthermore, one of Chinook's wins came
from a 10-ply series of movies drawn from its endgame
database, which Anaconda with an 8-ply look-ahead could not
have anticipated. If Anaconda had had access to an endgame
database of the same quality as Chinook's, the outcome of
the tournament might well have been a victory for Anaconda,
four wins to three.) These results "provide good support
for the expert-level rating that Anaconda earned on
www.zone.com" (p.76), with an overall rating of 2030-2055,
comparable to the 2045 rating it earned by playing against
humans. While Anaconda is not an invulnerable player, it is
able to play competitively at the expert level and hold its
own against a variety of extremely skilled human checkers
players. When one considers the very simple fitness
criterion under which these results were obtained, the
emergence of Anaconda provides dramatic corroboration of
the power of evolution.
- Geophysics
Sambridge and Gallagher 1993
used a genetic algorithm to locate earthquake hypocenters
based on seismological data. (The hypocenter is the point
beneath the Earth's surface at which an earthquake begins.
The epicenter is the point on the surface directly above
the hypocenter.) This is an exceedingly complex task, since
the properties of seismic waves depend on the properties of
the rock layers through which they travel. The traditional
method for locating the hypocenter relies upon what is
known as a seismic inversion algorithm, which starts with a
best guess of the location, calculates the derivatives of
wave travel time with respect to source position, and
performs a matrix operation to provide an updated location.
This process is repeated until an acceptable solution is
reached. (This Post
of the Month, from November 2003, provides more
information.) However, this method requires derivative
information and is prone to becoming trapped on local
optima.
A location algorithm that does not depend on derivative
information or velocity models can avoid these shortfalls
by calculating only the forward problem - the difference
between observed and predicted wave arrival times for
different hypocenter locations. However, an exhaustive
search based on this method would be far too
computationally expensive. This, of course, is precisely
the type of optimization problem at which genetic
algorithms excel. Like all GAs, the one proposed by the
cited paper is parallel in nature - rather than
progressively perturbing a single hypocenter closer and
closer to the solution, it begins with a cloud of potential
hypocenters which shrinks over time to converge on a single
solution. The authors state that their approach "can
rapidly locate near optimal solutions without an exhaustive
search of the parameter space" (p.1467), displays "highly
organized behavior resulting in efficient search" and is "a
compromise between the efficiency of derivative based
methods and the robustness of a fully nonlinear exhaustive
search" (p.1469). The authors conclude that their genetic
algorithm is "efficient for truly global optimization"
(p.1488) and "a powerful new tool for performing robust
hypocenter location" (p.1489).
- Materials
engineering
Giro, Cyrillo and Galvão
2002 used genetic algorithms to design electrically
conductive carbon-based polymers known as polyanilines.
These polymers, a recently invented class of synthetic
materials, have "large technological potential
applications" and may open up windows onto "new fundamental
physical phenomena" (p.170). However, due to their high
reactivity, carbon atoms can form a virtually infinite
number of structures, making a systematic search for new
molecules with interesting properties all but impossible.
In this paper, the authors apply a GA-based approach to the
task of designing new molecules with pre-specified
properties, starting with a randomly generated population
of initial candidates. They conclude that their methodology
can be a "very effective tool" (p.174) to guide
experimentalists in the search for new compounds and is
general enough to be extended to the design of novel
materials belonging to virtually any class of
molecules.
Weismann, Hammel and Bäck
1998 applied evolutionary algorithms to a "nontrivial"
(p.162) industrial problem: the design of multilayer
optical coatings used for filters that reflect, transmit or
absorb light of specified frequencies. These coatings are
used in the manufacture of sunglasses, for example, or
compact discs. Their manufacture is a precise task: the
layers must be laid down in a particular sequence and
particular thicknesses to produce the desired result, and
uncontrollable environmental variations in the
manufacturing environment such as temperature, pollution
and humidity may affect the performance of the finished
product. Many local optima are not robust against such
variations, meaning that maximum product quality must be
paid for with higher rates of undesirable deviation. The
particular problem considered in this paper also had
multiple criteria: in addition to the reflectance, the
spectral composition (color) of the reflected light was
also considered.
The EA operated by varying the number of coating layers and
the thickness of each, and produced designs that were
"substantially more robust to parameter variation" (p.166)
and had higher average performance than traditional
methods. The authors conclude that "evolutionary algorithms
can compete with or even outperform traditional methods"
(p.167) of multilayer optical coating design, without
having to incorporate domain-specific knowledge into the
search function and without having to seed the population
with good initial designs.
One more use of GAs in the field of materials engineering
merits mention: Robin et al. 2003
used GAs to design exposure patterns for an electron
lithography beam, used to etch submicrometer-scale
structures onto integrated circuits. Designing these
patterns is a highly difficult task; it is cumbersome and
wasteful to determine them experimentally, but the high
dimensionality of the search space defeats most search
algorithms. As many as 100 parameters must be optimized
simultaneously to control the electron beam and prevent
scattering and proximity effects that would otherwise ruin
the fine structures being sculpted. The forward problem -
determining the resulting structure as a function of the
electron dose - is straightforward and easy to simulate,
but the inverse problem of determining the electron
dose to produce a given structure, which is what is being
solved here, is far harder and no deterministic solution
exists.
Genetic algorithms, which are "known to be able to find
good solutions to very complex problems of high
dimensionality" (p.75) without needing to be supplied with
domain-specific information on the topology of the search
landscape, were applied successfully to this problem. The
paper's authors employed a steady-state GA with
roulette-wheel selection in a computer simulation, which
yielded "very good optimized" (p.77) exposure patterns. By
contrast, a type of hill-climber known as a
simplex-downhill algorithm was applied to the same problem,
without success; the SD method quickly became trapped in
local optima which it could not escape, yielding solutions
of poor quality. A hybrid approach of the GA and SD methods
also could not improve on the results delivered by the GA
alone.
- Mathematics and
algorithmics
Although some of the most promising applications and
compelling demonstrations of GAs' power are in the field of
engineering design, they are also relevant to "pure"
mathematical problems. Haupt and Haupt
1998 (p.140) discuss the use of GAs to solve high-order
nonlinear partial differential equations, typically by
finding the values for which the equations equal zero, and
give as an example a near-perfect GA solution for the
coefficients of the fifth-order Super Korteweg-de Vries
equation.
Sorting a list of items into order is an important task in
computer science, and a sorting network is an
efficient way to accomplish this. A sorting network is a
fixed list of comparisons performed on a set of a given
size; in each comparison, two elements are compared and
exchanged if not in order. Koza et al.
1999, p. 952 used genetic programming to evolve minimal
sorting networks for 7-item sets (16 comparisons), 8-item
sets (19 comparisons), and 9-item sets (25 comparisons). Mitchell 1996, p.21, discusses the
use of genetic algorithms by W. Daniel Hillis to find a
61-comparison sorting network for a 16-item set, only one
step more than the smallest known. This latter example is
particularly interesting for two innovations it used:
diploid chromosomes, and more notably, host-parasite
coevolution. Both the sorting networks and the test cases
evolved alongside each other; sorting networks were given
higher fitness based on how many test cases they sorted
correctly, while test cases were given higher fitness based
on how many sorting networks they could "trick" into
sorting incorrectly. The GA with coevolution performed
significantly better than the same GA without it.
One final, noteworthy example of GAs in the field of
algorithmics can be found in Koza et
al. 1999, who used genetic programming to discover a
rule for the majority classification problem in
one-dimensional cellular automata that is better than all
known rules written by humans. A one-dimensional cellular
automaton can be thought of as a finite tape with a given
number of positions (cells) on it, each of which can hold
either the state 0 or the state 1. The automaton runs for a
given number of time steps; at each step, every cell
acquires a new value based on its previous value and the
value of its nearest neighbors. (The Game
of Life is a two-dimensional cellular automaton.) The
majority classification problem entails finding a table of
rules such that, if more than half the cells on the tape
are 1 initially, all the cells go to 1; otherwise all the
cells go to 0. The challenge lies in the fact that any
individual cell can only access information about its
nearest neighbors; therefore, good rule sets must somehow
find a way to transmit information about distant regions of
the tape.
It is known that a perfect solution to this problem does
not exist - no rule set can accurately classify all
possible initial configurations - but over the past twenty
years, there has been a long succession of increasingly
better solutions. In 1978, three researchers developed the
so-called GKL rule, which correctly classifies 81.6% of the
possible initial states. In 1993, a better rule with an
accuracy of 81.8% was discovered; in 1995, another rule
with accuracy of 82.178% was found. All of these rules
required significant work by intelligent, creative humans
to develop. By contrast, the best rule discovered by a run
of genetic programming, given in Koza
et al. 1999, p.973, has an overall accuracy of 82.326%
- better than any of the human-created solutions that have
been developed over the last two decades. The authors note
that their new rules are qualitatively different from
previously published rules, employing fine-grained internal
representations of state density and intricate sets of
signals for communicating information over long
distance.
- Military and law
enforcement
Kewley and Embrechts 2002 used
genetic algorithms to evolve tactical plans for military
battles. The authors note that "[p]lanning for a tactical
military battle is a complex, high-dimensional task which
often bedevils experienced professionals" (p.163), not only
because such decisions are usually made under high-stress
conditions, but also because even simple plans require a
great number of conflicting variables and outcomes to take
into account: minimizing friendly casualties, maximizing
enemy casualties, controlling desired terrain, conserving
resources, and so on. Human planners have difficulty
dealing with the complexities of this task and often must
resort to "quick and dirty" approaches, such as doing
whatever worked last time.
To overcome these difficulties, the authors of the cited
paper developed a genetic algorithm to automate the
creation of battle plans, in conjunction with a graphical
battle simulator program. The commander enters the
preferred outcome, and the GA automatically evolves a
battle plan; in the simulation used, factors such as the
topography of the land, vegetative cover, troop movement
speed, and firing accuracy were taken into account. In this
experiment, co-evolution was also used to improve the
quality of the solutions: battle plans for the enemy forces
evolved concurrently with friendly plans, forcing the GA to
correct any weaknesses in its own plan that an enemy could
exploit. To measure the quality of solutions produced by
the GA, they were compared to battle plans for the same
scenario produced by a group of "experienced military
experts... considered to be very capable of developing
tactical courses of action for the size forces used in this
experiment" (p.166). These seasoned experts both developed
their own plan and, when the GA's solution was complete,
were given a chance to examine it and modify it as they saw
fit. Finally, all the sets of plans were run multiple times
on the simulator to determine their average quality.
The results speak for themselves: the evolved solution
outperformed both the military experts' own plan and the
plan produced by their modifications to the GA's solution.
"...[T]he plans produced by automated algorithms had a
significantly higher mean performance than those generated
by experienced military experts" (p.161). Furthermore, the
authors note that the GA's plan made good tactical sense.
(It involved a two-pronged attack on the enemy position by
mechanized infantry platoons supported by attack
helicopters and ground scouts, in conjunction with unmanned
aerial vehicles conducting reconnaissance to direct
artillery fire.) In addition, the evolved plan included
individual friendly units performing doctrinal missions -
an emergent property that appeared during the course of the
run, rather than being specified by the experimenter. In
increasingly networked modern battlefields, the attractive
potential of an evolutionary algorithm that can automate
the production of high-quality tactical plans should be
obvious.
An interesting use of GAs in law enforcement was reported
in Naik 1996, which described the
"FacePrints" software, a project to help witnesses identify
and describe criminal suspects. The cliched image of the
police sketch artist drawing a picture of the suspect's
face in response to witnesses' promptings is a difficult
and inefficient method: most people are not good at
describing individual aspects of a person's face, such as
the size of the nose or shape of the jaw, but instead are
better at recognizing whole faces. FacePrints takes
advantage of this by using a genetic algorithm that evolves
pictures of faces based on databases of hundreds of
individual features that can be combined in a vast number
of ways. The program shows randomly generated face images
to witnesses, who pick the ones that most resemble the
person they saw; the selected faces are then mutated and
bred together to generate new combinations of features, and
the process repeats until an accurate portrait of the
suspect's face emerges. In one real-life robbery case, the
final portraits created by the three witnesses were
strikingly similar, and the resulting picture was printed
in the local paper.
- Molecular biology
In living things, transmembrane proteins are
proteins that protrude through a cellular membrane.
Transmembrane proteins often perform important functions
such as sensing the presence of certain substances outside
the cell or transporting them into the cell. Understanding
the behavior of a transmembrane protein requires
identifying the segment of that protein that is actually
embedded within the membrane, which is called the
transmembrane domain. Over the last two decades,
molecular biologists have published a succession of
increasingly accurate algorithms for this purpose.
All proteins used by living things are made up of the same
20 amino acids. Some of these amino acids are
hydrophobic, meaning they are repelled by water, and
some are hydrophilic, meaning they are attracted to
water. Amino acid sequences that are part of a
transmembrane domain are more likely to be hydrophobic.
However, hydrophobicity is not a precisely defined
characteristic, and there is no one agreed-upon scale for
measuring it.
Koza et al. 1999, chapter 16, used
genetic programming to design an algorithm to identify
transmembrane domains of a protein. Genetic programming was
given a set of standard mathematical operators to work
with, as well as a set of boolean amino-acid-detecting
functions that return +1 if the amino acid at a given
position is the amino acid they detect and otherwise return
-1. (For example, the A? function takes as an argument one
number corresponding to a position within the protein, and
returns +1 if the amino acid at that position is alanine,
which is denoted by the letter A; otherwise it returns -1).
A single shared memory variable kept a running count of the
overall sum, and when the algorithm completed, the protein
segment was identified as a transmembrane domain if its
value was positive. Given only these tools, would it entail
the creation of new information for a human designer to
produce an efficient solution to this problem?
The solutions produced by genetic programming were
evaluated for fitness by testing them on 246 protein
segments whose transmembrane status was known. The
best-of-run individual was then evaluated on 250
additional, out-of-sample, test cases and compared to the
performance of the four best known human-written algorithms
for the same purpose. The result: Genetic programming
produced a transmembrane segment-identifying algorithm with
an overall error rate of 1.6% - significantly lower than
all four human-written algorithms, the best of which had an
error rate of 2.5%. The genetically designed algorithm,
which the authors dubbed the 0-2-4 rule, operates as
follows:
- Increment the running sum by 4 for each instance of
glutamic acid (an electrically charged and highly
hydrophilic) amino acid in the protein segment.
- Increment the running sum by 0 for each instance of
alanine, phenylalanine, isoleucine, leucine, methionine, or
valine (all highly hydrophobic amino acids) in the
protein segment.
- Increment the running sum by 2 for each instance of all
other amino acids.
- If [(SUM - 3.1544)/0.9357] is less than the length of
the protein segment, classify that segment as a
transmembrane domain; otherwise, classify it as a
nontransmembrane domain.
- Pattern recognition and
data mining
Competition in the telecommunications industry today is
fierce, and a new term - "churn" - has been coined to
describe the rapid rate at which subscribers switch from
one service provider to another. Churn costs telecom
carriers a large amount of money each year, and reducing
churn is an important factor in increasing profitability.
If carriers can contact customers who are likely to switch
and offer them special incentives to stay, churn rates can
be reduced; but no carrier has the resources to contact
more than a small percent of its customers. The problem is
therefore how to identify customers who are more likely to
churn. All carriers have extensive databases of customer
information that can theoretically be used for this
purpose; but what method works best for sifting through
this vast amount of data to identify the subtle patterns
and trends that signify a customer's likelihood of
churning?
Au, Chan and Yao 2003 applied genetic
algorithms to this problem to generate a set of if-then
rules that predict the churning probability of different
groups of customers. In their GA, the first generation of
rules, all of which had one condition, was generated using
a probabilistic induction technique. Subsequent generations
then refine these, combining simple, single-condition rules
into more complex, multi-condition rules. The fitness
measure used an objective "interestingness" measure of
correlation which requires no subjective input. The
evolutionary data-mining algorithm was tested on a
real-world database of 100,000 subscribers provided by a
Malaysian carrier, and its performance was compared against
two alternative methods: a multilayer neural network and a
widely used decision-tree-based algorithm, C4.5. The
authors state that their EA was able to discover hidden
regularities in the database and was "able to make accurate
churn prediction under different churn rates" (p.542),
outperforming C4.5 under all circumstances, outperforming
the neural network under low monthly churn rates and
matching the neural network under larger churn rates, and
reaching conclusions more quickly in both cases. Some
further advantages of the evolutionary approach are that it
can operate efficiently even when some data fields are
missing and that it can express its findings in easily
understood rule sets, unlike the neural net.
Among some of the more interesting rules discovered by the
EA are as follows: subscribers are more likely to churn if
they are personally subscribed to the service plan and have
not been admitted to any bonus scheme (a potential solution
is to admit all such subscribers to bonus schemes);
subscribers are more likely to churn if they live in Kuala
Lumpur, are between 36 and 44 in age, and pay their bills
with cash (presumably because it is easier for subscribers
who pay cash, rather than those whose accounts are
automatically debited, to switch providers); and
subscribers living in Penang who signed up through a
certain dealer are more likely to churn (this dealer may be
providing poor customer service and should be
investigated).
Rizki, Zmuda and Tamburino 2002
used evolutionary algorithms to evolve a complex pattern
recognition system with a wide variety of potential uses.
The authors note that the task of pattern recognition is
increasingly being performed by machine learning
algorithms, evolutionary algorithms in particular. Most
such approaches begin with a pool of predefined features,
from which an EA can select appropriate combinations for
the task at hand; by contrast, this approach began from the
ground up, first evolving individual feature detectors in
the form of expression trees, then evolving cooperative
combinations of those detectors to produce a complete
pattern recognition system. The evolutionary process
automatically selects the number of feature detectors, the
complexity of the detectors, and the specific aspects of
the data each detector responds to.
To test their system, the authors gave it the task of
classifying aircraft based on their radar reflections. The
same kind of aircraft can return quite different signals
depending on the angle and elevation at which it is viewed,
and different kinds of aircraft can return very similar
signals, so this is a non-trivial task. The evolved pattern
recognition system correctly classified 97.2% of the
targets, a higher net percentage than any of the three
other techniques - a perceptron neural network, a
nearest-neighbor classifier algorithm, and a radial basis
algorithm - against which it was tested. (The radial basis
network's accuracy was only 0.5% less than the evolved
classifier, which is not a statistically significant
difference, but the radial basis network required 256
feature detectors while the evolved recognition system used
only 17.) As the authors state, "The recognition systems
that evolve use fewer features than systems formed using
conventional techniques, yet achieve comparable or superior
recognition accuracy" (p.607). Various aspects of their
system have also been applied to problems including optical
character recognition, industrial inspection and medical
image analysis.
Hughes and Leyland 2000 also
applied multiple-objective GAs to the task of classifying
targets based on their radar reflections. High-resolution
radar cross section data requires massive amounts of disk
storage space, and it is very computationally intensive to
produce an actual model of the source from the data. By
contrast, the authors' GA-based approach proved very
successful, producing a model as good as the traditional
iterative approach while reducing the computational
overhead and storage requirements to the point where it was
feasible to generate good models on a desktop computer. By
contrast, the traditional iterative approach requires ten
times the resolution and 560,000 times as many accesses of
image data to produce models of similar quality. The
authors conclude that their results "clearly demonstrate"
(p.160) the ability of the GA to process both two- and
three-dimensional radar data of any level of resolution
with far fewer calculations than traditional methods, while
retaining acceptably high accuracy.
- Robotics
The international RoboCup tournament is a
project to promote advances in robotics, artificial
intelligence, and related fields by providing a standard
problem where new technologies can be tried out -
specifically, it is an annual soccer tournament between
teams of autonomous robots. (The stated goal is to develop
a team of humanoid robots that can win against the
world-champion human soccer team by 2050; at the present
time, most of the competing robot teams are wheeled.) The
programs that control the robotic team members must display
complex behavior, deciding when to block, when to kick, how
to move, when to pass the ball to teammates, how to
coordinate defense and offense, and so on. In the simulator
league of the 1997 competition, David Andre and Astro
Teller entered a team named Darwin United whose control
programs had been developed automatically from the ground
up by genetic programming, a challenge to the conventional
wisdom that "this problem is just too difficult for such a
technique" (Andre and Teller 1999,
p. 346).
To solve this difficult problem, Andre and Teller provided
the genetic programming algorithm with a set of primitive
control functions such as turning, moving, kicking, and so
on. (These functions were themselves subject to change and
refinement during the course of evolution.) Their fitness
function, written to reward good play in general rather
than scoring specifically, provided a list of increasingly
important objectives: getting near the ball, kicking the
ball, keeping the ball on the opponent's side of the field,
moving in the correct direction, scoring goals, and winning
the game. It should be noted that no code was provided to
teach the team specifically how to achieve these
complex objectives. The evolved programs were then
evaluated using a hierarchical selection model: first, the
candidate teams were tested on an empty field and rejected
if they did not score a goal within 30 seconds. Next, they
were evaluated against a team of stationary "kicking posts"
that kick the ball toward the opposite side of the field.
Thirdly, the team played a game against the winning team
from the RoboCup 1997 competition. Finally, teams that
scored at least one goal against this team were played off
against each other to determine which was best.
Out of 34 teams in its division, Darwin United ultimately
came in 17th, placing squarely in the middle of the field
and outranking half of the human-written entries. While a
tournament victory would undoubtedly have been more
impressive, this result is competitive and significant in
its own right, and appears even more so in the light of
history. About 25 years ago, chess-playing computer
programs were in their infancy; a computer had only
recently entered even a regional competition for the first
time, although it did not win (Sagan
1979, p.286). But "[a] machine that plays chess in the
middle range of human expertise is a very capable machine"
(ibid.), and it might be said that the same is true of
robot soccer. Just as chess-playing machines compete at
world grandmaster levels today, what types of systems will
genetic programming be producing 20 or 30 years from
now?
- Routing and
scheduling
Burke and Newall 1999 used genetic
algorithms to schedule exams among university students. The
timetable problem in general is known to be NP-complete,
meaning that no method is known to find a
guaranteed-optimal solution in a reasonable amount of time.
In such a problem, there are both hard constraints - two
exams may not be assigned to the same room at the same time
- and soft constraints - students should not be assigned to
multiple exams in succession, if possible, to minimize
fatigue. Hard constraints must be satisfied, while soft
constraints should be satisfied as far as possible. The
authors dub their hybrid approach for solving this problem
a "memetic algorithm": an evolutionary algorithm with
rank-based, fitness-proportionate selection, combined with
a local hill-climber to optimize solutions found by the EA.
The EA was applied to data sets from four real universities
(the smallest of which had an enrollment of 25,000
students), and its results were compared to results
produced by a heuristic backtracking method, a
well-established algorithm that is among the best known for
this problem and that is used at several real universities.
Compared to this method, the EA produced a result with a
quite uniform 40% reduction in penalty.
He and Mort 2000 applied genetic
algorithms to the problem of finding optimal routing paths
in telecommunications networks (such as phone networks and
the Internet) which are used to relay data from senders to
recipients. This is an NP-hard optimization problem, a type
of problem for which GAs are "extremely well suited... and
have found an enormous range of successful applications in
such areas" (p.42). It is also a multiobjective problem,
balancing conflicting objectives such as maximizing data
throughput, minimizing transmission delay and data loss,
finding low-cost paths, and distributing the load evenly
among routers or switches in the network. Any successful
real-world algorithm must also be able to re-route around
primary paths that fail or become congested.
In the authors' hybrid GA, a shortest-path-first algorithm,
which minimizes the number of "hops" a given data packet
must pass through, is used to generate the seed for the
initial population. However, this solution does not take
into account link congestion or failure, which are
inevitable conditions in real networks, and so the GA takes
over, swapping and exchanging sections of paths. When
tested on a data set derived from a real Oracle network
database, the GA was found to be able to efficiently route
around broken or congested links, balancing traffic load
and maximizing the total network throughput. The authors
state that these results demonstrate the "effectiveness and
scalability" of the GA and show that "optimal or
near-optimal solutions can be achieved" (p.49).
This technique has found real-world applications for
similar purposes, as reported in Begley and Beals 1995. The
telecommunications company U.S. West (now merged with
Qwest) was faced with the task of laying a network of
fiber-optic cable. Until recently, the problem of designing
the network to minimize the total length of cable laid was
solved by an experienced engineer; now the company uses a
genetic algorithm to perform the task automatically. The
results: "Design time for new networks has fallen from two
months to two days and saves US West $1 million to $10
million each" (p.70).
Jensen 2003 and Chryssolouris and Subramaniam
2001 applied genetic algorithms to the task of
generating schedules for job shops. This is an NP-hard
optimization problem with multiple criteria: factors such
as cost, tardiness, and throughput must all be taken into
account, and job schedules may have to be rearranged on the
fly due to machine breakdowns, employee absences, delays in
delivery of parts, and other complications, making
robustness in a schedule an important consideration. Both
papers concluded that GAs are significantly superior to
commonly used dispatching rules, producing efficient
schedules that can more easily handle delays and
breakdowns. These results are not merely theoretical, but
have been applied to real-world situations:
As reported in Naik 1996,
organizers of the 1992 Paralympic Games used a GA to
schedule events. As reported in Petzinger 1995, John Deere &
Co. has used GAs to generate schedules for a Moline,
Illinois plant that manufactures planters and other heavy
agricultural equipment. Like luxury cars, these can be
built in a wide variety of configurations with many
different parts and options, and the vast number of
possible ways to build them made efficient scheduling a
seemingly intractable problem. Productivity was hampered by
scheduling bottlenecks, worker teams were bickering, and
money was being lost. Finally, in 1993, Deere turned to
Bill Fulkerson, a staff analyst and engineer who conceived
of using a genetic algorithm to produce schedules for the
plant. Overcoming initial skepticism, the GA quickly proved
itself: monthly output has risen by 50 percent, overtime
has nearly vanished, and other Deere plants are
incorporating GAs into their own scheduling.
As reported in Rao 1998, Volvo has
used an evolutionary program called OptiFlex to schedule
its million-square-foot factory in Dublin, Virginia, a task
that requires handling hundreds of constraints and millions
of possible permutations for each vehicle. Like all genetic
algorithms, OptiFlex works by randomly combining different
scheduling possibilities and variables, determines their
fitness by ranking them according to costs, benefits and
constraints, then causes the best solutions to swap genes
and sends them back into the population for another trial.
Until recently, this daunting task was handled by a human
engineer who took up to four days to produce the schedule
for each week; now, thanks to GAs, this task can be
completed in one day with minimal human intervention.
As reported in Lemley 2001,
United Distillers and Vintners, a Scottish company that is
the largest and most profitable spirits distributor in the
world and accounts for over one-third of global grain
whiskey production, uses a genetic algorithm to manage its
inventory and supply. This is a daunting task, requiring
the efficient storage and distribution of over 7 million
barrels containing 60 distinct recipes among a vast system
of warehouses and distilleries, depending on a multitude of
factors such as age, malt number, wood type and market
conditions. Previously, coordinating this complex flow of
supply and demand required five full-time employees. Today,
a few keystrokes on a computer instruct a genetic algorithm
to generate a new schedule each week, and warehouse
efficiency has nearly doubled.
Beasley, Sonander and Havelock
2001 used a GA to schedule airport landings at London
Heathrow, the United Kingdom's busiest airport. This is a
multiobjective problem that involves, among other things,
minimizing delays and maximizing number of flights while
maintaining adequate separation distances between planes
(air vortices that form in a plane's wake can be dangerous
to another flying too closely behind). When compared to
actual schedules from a busy period at the airport, the GA
was able to reduce average wait time by 2-5%, equating to
one to three extra flights taking off and landing per hour
- a significant improvement. However, even greater
improvements have been achieved: as reported in Wired 2002, major international
airports and airlines such as Heathrow, Toronto, Sydney,
Las Vegas, San Francisco, America West Airlines,
AeroMexico, and Delta Airlines are using genetic algorithms
to schedule takeoffs, landings, maintenance and other
tasks, in the form of Ascent Technology's SmartAirport
Operations Center software (see http://www.ascent.com/faq.html).
Breeding and mutating solutions in the form of schedules
that incorporate thousands of variables, "Ascent beats
humans hands-down, raising productivity by up to 30 percent
at every airport where it's been implemented."
- Systems
engineering
Benini and Toffolo 2002 applied a
genetic algorithm to the multi-objective task of designing
wind turbines used to generate electric power. This design
"is a complex procedure characterized by several trade-off
decisions... The decision-making process is very difficult
and the design trends are not uniquely established"
(p.357); as a result, there are a number of different
turbine types in existence today and no agreement on which,
if any, is optimal. Mutually exclusive objectives such as
maximum annual energy production and minimal cost of energy
must be taken into account. In this paper, a
multi-objective evolutionary algorithm was used to find the
best trade-offs between these goals, constructing turbine
blades with the optimal configuration of characteristics
such as tip speed, hub/tip ratio, and chord and twist
distribution. In the end, the GA was able to find solutions
competitive with commercial designs, as well as more
clearly elucidate the margins by which annual energy
production can be improved without producing overly
expensive designs.
Haas, Burnham and Mills 1997 used a
multiobjective genetic algorithm to optimize the beam
shape, orientation and intensity of X-ray emitters used in
targeted radiotherapy to destroy cancerous tumors while
sparing healthy tissue. (X-ray photons aimed at a tumor
tend to be partially scattered by structures within the
body, unintentionally damaging internal organs. The
challenge is to minimize this effect while maximizing the
radiation dose delivered to the tumor.) Using a rank-based
fitness model, the researchers began with the solution
produced by the conventional method, an iterative
least-squares approach, and then used the GA to modify and
improve it. By constructing a model of a human body and
exposing it to the beam configuration evolved by the GA,
they found good agreement between the predicted and actual
distributions of radiation. The authors conclude that their
results "show a sparing of [healthy organs] that could not
be achieved using conventional techniques" (p.1745).
Lee and Zak 2002 used a genetic
algorithm to evolve a set of rules to control an automotive
anti-lock braking system. While the ability of antilock
brake systems to reduce stopping distance and improve
maneuverability has saved many lives, the performance of an
ABS is dependent on road surface conditions: for example,
an ABS controller that is optimized for dry asphalt will
not work as well on wet or icy roads, and vice versa. In
this paper, the authors propose a GA to fine-tune an ABS
controller that can identify the road surface properties
(by monitoring wheel slip and acceleration) and respond
accordingly, delivering the appropriate amount of braking
force to maximize the wheels' traction. In testing, the
genetically tuned ABS "exhibits excellent tracking
properties" (p.206) and was "far superior" (p.209) to two
other methods of braking maneuvers, quickly finding new
optimal values for wheel slip when the type of terrain
changes beneath a moving car and reducing total stopping
distance. "The lesson we learned from our experiment... is
that a GA can help to fine-tune even a well-designed
controller. In our case, we already had a good solution to
the problem; yet, with the help of a GA, we were able to
improve the control strategy significantly. In summary, it
seems that it is worthwhile to try to apply a GA, even to a
well-designed controller, because there is a good chance
that one can find a better set of the controller settings
using GAs" (p.211).
As cited in Schechter 2000,
Dr. Peter Senecal of the University of Wisconsin used
small-population genetic algorithms to improve the
efficiency of diesel engines. These engines work by
injecting fuel into a combustion chamber which is filled
with extremely compressed and therefore extremely hot air,
hot enough to cause the fuel to explode and drive a piston
that produces the vehicle's motive force. This basic design
has changed little since it was invented by Rudolf Diesel
in 1893; although vast amounts of effort have been put into
making improvements, this is a very difficult task to
perform analytically because it requires precise knowledge
of the turbulent behavior displayed by the fuel-air mixture
and simultaneous variation of many interdependent
parameters. Senecal's approach, however, eschewed the use
of such problem-specific knowledge and instead worked by
evolving parameters such as the pressure of the combustion
chamber, the timing of the fuel injections and the amount
of fuel in each injection. The result: the simulation
produced an improved engine that consumed 15% less fuel
than a normal diesel engine and produced one-third as much
nitric oxide exhaust and half as much soot. Senecal's team
then built a real diesel engine according to the
specifications of the evolved solution and got the same
results. Senecal is now moving on to evolving the geometry
of the engine itself, hopefully producing even greater
improvements.
As cited in Begley and Beals
1995, Texas Instruments used a genetic algorithm to
optimize the layout of components on a computer chip,
placing structures so as to minimize the overall area and
create the smallest chip possible. Using a connection
strategy that no human had thought of, the GA came up with
a design that took 18% less space.
Finally, as cited in Ashley 1992,
a proprietary software system known as Engineous that
employs genetic algorithms is being used by companies in
the aerospace, automotive, manufacturing, turbomachinery
and electronics industries to design and improve engines,
motors, turbines and other industrial devices. In the words
of its creator, Dr. Siu Shing Tong, Engineous is "a master
'tweaker,' tirelessly trying out scores of 'what-if'
scenarios until the best possible design emerges" (p.49).
In one trial of the system, Engineous was able to produce a
0.92 percent increase in the efficiency of an experimental
turbine in only one week, while ten weeks of work by a
human designer produced only a 0.5 percent
improvement.
Granted, Engineous does not rely solely on genetic
algorithms; it also employs numerical optimization
techniques and expert systems which use logical if-then
rules to mimic the decision-making process of a human
engineer. However, these techniques are heavily dependent
on domain-specific knowledge, lack general applicability,
and are prone to becoming trapped on local optima. By
contrast, the use of genetic algorithms allows Engineous to
explore regions of the search space that other methods
miss.
Engineous has found widespread use in a variety of
industries and problems. Most famously, it was used to
improve the turbine power plant of the Boeing 777 airliner;
as reported in Begley and Beals
1995, the genetically optimized design was almost 1%
more fuel-efficient than previous engines, which in a field
such as this is "a windfall". Engineous has also been used
to optimize the configuration of industrial DC motors,
hydroelectric generators and steam turbines, to plan out
power grids, and to design superconducting generators and
nuclear power plants for orbiting satellites. Rao 1998 also reports that NASA has
used Engineous to optimize the design of a high-altitude
airplane for sampling ozone depletion, which must be both
light and efficient.
As one might expect, the real-world demonstration of the
power of evolution that GAs represent has proven surprising
and disconcerting for creationists, who have always claimed
that only intelligent design, not random variation and
selection, could have produced the information content and
complexity of living things. They have therefore argued
that the success of genetic algorithms does not allow us to
infer anything about biological evolution. The criticisms
of two anti-evolutionists, representing two different
viewpoints, will be addressed: young-earth creationist Dr.
Don Batten of Answers in Genesis, who has written an
article entitled "
Genetic algorithms -- do they show that evolution
works?", and old-earth creationist and
intelligent-design advocate Dr. William Dembski, whose
recent book No Free Lunch (Dembski 2002) discusses this
topic.
Don Batten
- Some traits in living
things are qualitative, whereas GAs are always
quantitative
Batten states that GAs must be quantitative, so that any
improvement can be selected for. This is true. He then goes
on to say, "Many biological traits are qualitative--it
either works or it does not, so there is no step-wise means
of getting from no function to the function." This
assertion has not been demonstrated, however, and is not
supported by evidence. Batten does not even attempt to give
an example of a biological trait that either "works or does
not" and thus cannot be built up in a stepwise
fashion.
But even if he did offer such a trait, how could he
possibly prove that there is no stepwise path to it?
Even if we do not know of such a path, does it follow that
there is none? Of course not. Batten is effectively
claiming that if we do not understand how certain traits
evolved, then it is impossible for those traits to have
evolved - a classic example of the elementary logical
fallacy of argument from ignorance. The search space
of all possible variants of any given biological trait is
enormous, and in most cases our knowledge subsumes only an
infinitesimal fraction of the possibilities. There may well
be numerous paths to a structure which we do not yet know
about; there is no reason whatsoever to believe our current
ignorance sets limits on our future progress. Indeed,
history gives us reason to be confident: scientists have
made enormous progress in explaining the evolution of
many complex biological structures and systems, both
macroscopic and microscopic (for example, see these pages
on the evolution of complex molecular
systems, "clock" genes, the woodpecker's
tongue or the
bombardier beetle). We are justified in believing it
likely that the ones that have so far eluded us will also
be made clear in the future.
In fact, GAs themselves give us an excellent reason to
believe this. Many of the problems to which they have been
applied are complex engineering and design issues where the
solution was not known ahead of time and therefore the
problem could not be "rigged" to aid the algorithm's
success. If the creationists were correct, it would have
been entirely reasonable to expect genetic algorithms to
fail dismally time after time when applied to these
problems, but instead, just the opposite has occurred: GAs
have discovered powerful, high-quality solutions to
difficult problems in a diverse variety of fields. This
calls into serious question whether there even are any
problems such as Batten describes, whose solutions are
inaccessible to an evolutionary process.
- GAs select for
one trait at a time, whereas living things are
multidimensional
Batten states that in GAs, "A single trait is selected for,
whereas any living thing is multidimensional", and asserts
that in living things with hundreds of traits, "selection
has to operate on all traits that affect survival",
whereas "[a] GA will not work with three or four different
objectives, or I dare say even just two."
This argument reveals Batten's profound ignorance of the
relevant literature. Even a cursory survey of the work done
on evolutionary algorithms (or a look at an earlier section of this
essay) would have revealed that multiobjective
genetic algorithms are a major, thriving area of
research within the broader field of evolutionary
computation and prevented him from making such an
embarrassingly incorrect claim. There are journal articles,
entire issues of prominent journals on evolutionary
computation, entire conferences, and entire books on the
topic of multiobjective GAs. Coello
2000 provides a very extensive survey, with five pages
of references to papers on the use of multiobjective
genetic algorithms in a broad range of fields; see also Fleming and Purshouse 2002; Hanne 2000; Zitzler and Thiele 1999; Fonseca and Fleming 1995; Srinivas and Deb 1994; Goldberg 1989, p.197. For some
books and papers discussing the use of multiobjective GAs
to solve specific problems, see: Obayashi et al. 2000; Sasaki et al. 2001; Benini and Toffolo 2002; Haas, Burnham and Mills 1997; Chryssolouris and Subramaniam
2001; Hughes and Leyland
2000; He and Mort 2000; Kewley and Embrechts 2002; Beasley, Sonander and Havelock
2001; Sato et al. 2002; Tang et al. 1996; Williams, Crossley and Lang 2001;
Koza et al. 1999; Koza et al. 2003. For a comprehensive
repository of citations on multiobjective GAs, see http://www.lania.mx/~ccoello/EMOO/.
- GAs do not allow the
possibility of extinction or error catastrophe
Batten claims that, in GAs, "Something always
survives to carry on the process", while this is not
necessarily true in the real world - in short, GAs do not
allow the possibility of extinction.
However, this is not true; extinction can occur. For
example, some GAs use a model of selection called
thresholding, in which individuals must have a
fitness higher than some predetermined level to survive and
reproduce (Haupt and Haupt 1998,
p. 37). If no individual meets this standard in such a GA,
the population can indeed go extinct. But even in GAs that
do not use thresholding, states analogous to extinction can
occur. If mutation rates are too high or selective
pressures too strong, then a GA will never find a feasible
solution. The population may become hopelessly scrambled as
deleterious mutations building up faster than selection can
remove them disrupt fitter candidates (error catastrophe),
or it may thrash around helplessly, unable to achieve any
gain in fitness large enough to be selected for. Just as in
nature, there must be a balance or a solution will never be
reached. The one advantage a programmer has in this respect
is that, if this does happen, he can reload the program
with different values - for population size, for mutation
rate, for selection pressure - and start over again.
Obviously this is not an option for living things. Batten
says, "There is no rule in evolution that says that some
organism(s) in the evolving population will remain viable
no matter what mutations occur," but there is no such rule
in genetic algorithms either.
Batten also states that "the GAs that I have looked at
artificially preserve the best of the previous generation
and protect it from mutations or recombination in case
nothing better is produced in the next iteration". This
criticism will be addressed in the next point.
- GAs ignore the cost of
substitution
Batten's next claim is that GAs neglect "Haldane's Dilemma", which
states that an allele which contributes less to an
organism's fitness will take a correspondingly longer time
to become fixated in a population. Obviously, what he is
referring to is the elitist selection technique, which
automatically selects the best candidate at each generation
no matter how small its advantage over its competitors is.
He is right to suggest that, in nature, very slight
competitive advantages might take much longer to propagate.
Genetic algorithms are not an exact model of biological
evolution in this respect.
However, this is beside the point. Elitist selection is an
idealization of biological evolution - a model of
what would happen in nature if chance did not
intervene from time to time. As Batten acknowledges,
Haldane's dilemma does not state that a slightly
advantageous mutation will never become fixed in a
population; it states that it will take more time for it to
do so. However, when computation time is at a premium or a
GA researcher wishes to obtain a solution more quickly, it
may be desirable to skip this process by implementing
elitism. An important point is that elitism does not affect
which mutations arise, merely makes certain the
selection of the best ones that do arise. It would
not matter what the strength of selection was if
information-increasing mutations did not occur. In other
words, elitism speeds up convergence once a good solution
has been discovered - it does not bring about an outcome
which would not otherwise have occurred. Therefore, if
genetic algorithms with elitism can produce new
information, then so can evolution in the wild.
Furthermore, not all GAs use elitist selection. Many do
not, instead relying only on roulette-wheel selection and
other stochastic sampling techniques, and yet these have
been no less successful. For instance, Koza et al. 2003, p.8-9, gives
examples of 36 instances where genetic programming has
produced human-competitive results, including the automated
recreation of 21 previously patented inventions (six of
which were patented during or after 2000), 10 of which
duplicate the functionality of the patent in a new way, and
also including two patentable new inventions and five new
algorithms that outperform any human-written algorithms for
the same purpose. As Dr. Koza states in an earlier
reference to the same work (1999,
p.1070): "The elitist strategy is not used." Some other
papers cited in this essay in which elitism is not used
include: Robin et al. 2003; Rizki, Zmuda and Tamburino 2002; Chryssolouris and Subramaniam
2001; Burke and Newall 1999;
Glen and Payne 1995; Au, Chan and Yao 2003; Jensen 2003; Kewley and Embrechts 2002; Williams, Crossley and Lang 2001;
Mahfoud and Mani 1996. In each
of these cases, without any mechanism to ensure that the
best individuals were selected at each generation, without
exempting these individuals from potentially detrimental
random change, genetic algorithms still produce
powerful, efficient, human-competitive results. This fact
may be surprising to creationists such as Batten, but it is
wholly expected by advocates of evolution.
- GAs ignore generation
time constraints
This criticism is puzzling. Batten claims that a single
generation in a GA can take microseconds, whereas a single
generation in any living organism can take anywhere from
minutes to years. This is true, but how it is supposed to
bear on the validity of GAs as evidence for evolution is
not explained. If a GA can generate new information,
regardless of how long it takes, then surely evolution in
the wild can do so as well; that GAs can indeed do so is
all this essay intends to demonstrate. The only remaining
issue would then be whether biological evolution has
actually had enough time to cause significant change, and
the answer to this question would be one for biologists,
geologists and physicists, not computer programmers.
The answer these scientists have provided is fully in
accord with evolutionary timescales, however. Numerous
lines of independent evidence, including radiometric
isochron dating, the
cooling rates of white dwarfs, the nonexistence of
isotopes with short halflives in nature, the recession
rates of distant galaxies, and
analysis of the cosmic microwave background radiation
all converge on the same conclusion: an Earth and a
universe many billions of years old, easily long enough for
evolution to produce all the diversity of life we see today
by all reasonable estimates.
- GAs employ
unrealistically high rates of mutation and
reproduction
Batten asserts, without providing any supporting evidence
or citations, that GAs "commonly produce 100s or 1000s of
'offspring' per generation", a rate even bacteria, the
fastest-reproducing biological organisms, cannot
match.
This criticism misses the mark in several ways. First of
all, if the metric being used is (as it should be) number
of offspring per generation, rather than number of
offspring per unit of absolute time, then there clearly are
biological organisms that can reproduce at rates faster
than that of bacteria and roughly equal to the rates Batten
claims are unrealistic. For example, a single frog can lay
thousands of eggs at a time, each of which has the
potential to develop into an adult. Granted, most of these
usually will not survive due to resource limitations and
predation, but then most of the "offspring" in each
generation of a GA will not go on either.
Secondly, and more importantly, a genetic algorithm working
on solving a problem is not meant to represent a single
organism. Instead, a genetic algorithm is more analogous to
an entire population of organisms - after all, it is
populations, not individuals, that evolve. Of course, it is
eminently plausible for a whole population to collectively
have hundreds or thousands of offspring per generation.
(Creationist Walter ReMine makes this same mistake with
regards to Dr. Richard Dawkins' "weasel" program. See this
Post of the Month for more.)
Additionally, Batten says, the mutation rate is
artificially high in GAs, whereas living organisms have
error-checking machinery designed to limit the mutation
rate to about 1 in 10 billion base pairs (though this is
too small - the actual figure is closer to 1 in 1 billion.
See Dawkins 1996, p.124). Now of
course this is true. If GAs mutated at this rate, they
would take far too long to solve real-world problems.
Clearly, what should be considered relevant is the rate of
mutation relative to the size of the genome. The
mutation rate should be high enough to promote a sufficient
amount of diversity in the population without overwhelming
the individuals. An average human will possess between one
and five mutations; this is not at all unrealistic for the
offspring in a GA.
- GAs have
artificially small genomes
Batten's argument that the genome of a genetic algorithm
"is artificially small and only does one thing" is badly
misguided. In the first place, as we have seen, it is
not true that a GA only does one thing; there are
many examples of genetic algorithms specifically designed
to optimize many parameters simultaneously, often far more
parameters simultaneously than a human designer ever
could.
And how exactly does Batten quantify "artificially small"?
Many evolutionary algorithms, such as John Koza's genetic
programming, use variable-length encodings where the size
of candidate solutions can grow arbitrarily large. Batten
claims that even the simplest living organism has far more
information in its genome than a GA has ever produced, but
while organisms living today may have relatively
large genomes, that is because much complexity has been
gained over the course of billions of years of evolution.
As the Probability
of Abiogenesis article points out, there is good reason
to believe that the earliest living organisms were very
much simpler than any species currently extant -
self-replicating molecules probably no longer than 30 or 40
subunits, which could easily be specified by the 1800 bits
of information that Batten apparently concedes at least one
GA has generated. Genetic algorithms are similarly a very
new technique whose full potential has not yet been tapped;
digital computers themselves are only a few decades old,
and as Koza (2003, p. 25) points
out, evolutionary computing techniques have been generating
increasingly more substantial and complex results over the
last 15 years, in synchrony with the ongoing rapid increase
in computing power often referred to as "Moore's
Law". Just as early life was very simple compared to
what came after, today's genetic algorithms, despite the
impressive results they have already produced, are likely
to give rise to far greater things in the future.
- GAs ignore
the possibility of mutation occurring throughout the
genome
Batten apparently does not understand how genetic
algorithms work, and he shows it by making this argument.
He states that in real life, "mutations occur throughout
the genome, not just in a gene or section that specifies a
given trait". This is true, but when he says that the same
is not true of GAs, he is wrong. Exactly like in living
organisms, GAs permit mutation and recombination to occur
anywhere in the genomes of their candidate solutions;
exactly like in living organisms, GAs must weed out the
deleterious changes while simultaneously selecting for the
beneficial ones.
Batten goes on to claim that "the program itself is
protected from mutations; only target sequences are
mutated", and if the program itself were mutated it would
soon crash. This criticism, however, is irrelevant. There
is no reason why the governing program of a GA should be
mutated. The program is not part of the genetic algorithm;
the program is what supervises the genetic algorithm and
mutates the candidate solutions, which are what the
programmer is seeking to improve. The program running the
GA is not analogous to the reproductive machinery of an
organism, a comparison which Batten tries to make. Rather,
it is analogous to the invariant natural laws that govern
the environments in which living organisms live and
reproduce, and these are neither expected to change nor
need to be "protected" from it.
- GAs ignore problems of
irreducible complexity
Using old-earth creationist Michael Behe's
argument of "irreducible complexity", Batten argues,
"Many biological traits require many different components
to be present, functioning together, for the trait to exist
at all," whereas this does not happen in GAs.
However, it is trivial to show that such a claim is false,
as genetic algorithms have produced irreducibly
complex systems. For example, the voice-recognition circuit
Dr. Adrian Thompson evolved (Davidson 1997) is composed of 37
core logic gates. Five of them are not even connected to
the rest of the circuit, yet all 37 are required for the
circuit to work; if any of them are disconnected from their
power supply, the entire system ceases to function. This
fits Behe's definition of an irreducibly complex system and
shows that an evolutionary process can produce such
things.
It should be noted that this is the same argument as the
first one, merely presented in different language, and thus
the refutation is the same. Irreducible complexity is not a
problem for evolution, whether that evolution is occurring
in living beings in the wild or in silicon on a computer's
processor chip.
- GAs ignore polygeny,
pleiotropy, and other genetic complexity
Batten argues that GAs ignore issues of polygeny (the
determination of one trait by multiple genes), pleiotropy
(one gene affecting multiple traits), and dominant and
recessive genes.
However, none of these claims are true. GAs do not ignore
polygeny and pleiotropy: these properties are merely
allowed to arise naturally rather than being deliberately
coded in. It is obvious that in any complex interdependent
system (i.e., a nonlinear
system), the alteration or removal of one part will
cause a ripple effect of changes throughout; thus GAs
naturally incorporate polygeny and pleiotropy. "In the
genetic algorithm literature, parameter interaction is
called epistasis (a biological term for gene
interaction). When there is little to no epistasis, minimum
seeking algorithms [i.e., hill-climbers --A.M.] perform
best. Genetic algorithms shine when the epistasis is medium
to high..." (Haupt and Haupt 1998,
p. 31, original emphasis).
Likewise, there are some genetic algorithm implementations
that do have diploid chromosomes and dominant and recessive
genes (Goldberg 1989, p.150; Mitchell 1996, p.22). However,
those that do not are simply more like haploid organisms,
such as bacteria, than they are like diploid organisms,
such as human beings. Since (by certain measures) bacteria
are among the most successful organisms on this planet,
such GAs remain a good model of evolution.
- GAs do not have multiple
reading frames
Batten discusses the existence of multiple reading frames
in the genomes of some living things, in which the DNA
sequences code for different functional proteins when read
in different directions or with different starting offsets.
He asserts that "Creating a GA to generate such
information-dense coding would seem to be out of the
question".
Such a challenge begs for an answer, and here it is: Soule and Ball 2001. In this paper,
the authors present a genetic algorithm with multiple
reading frames and dense coding, enabling it to store more
information than the total length of its genome. Like the
three-nucleotide codons that specify amino acids in the
genomes of living organisms, this GA's codons were
five-digit binary strings. Since the
codons were five digits long, there were five different
possible reading frames. The sequence 11111 serves as a
"start" codon and 00000 as a "stop" codon; because the
start and stop codons could occur anywhere in the genome,
the length of each individual was variable. Regions of the
chromosome which did not fall between start-stop pairs were
ignored.
The GA was tested on four classic function maximization
problems. "Initially, the majority of the bits do not
participate in any gene, i.e., most of a chromosome is
non-coding. Again this is because in the initial random
individuals there are relatively few start-stop codon
pairs. However, the number of bits that do not participate
decreases extremely rapidly." During the course of the run,
the GA can increase the effective length of its genome by
introducing new start codons in different reading frames.
By the end of the run, "the amount of overlap is quite
high. Many bits are participating in several (and often all
five) genes." On all test problems, the GA started, on
average, with 5 variables specified; by the end of the run,
that number had increased to an average of around 25.
In the test problems, the GA with multiple reading frames
produced significantly better solutions than a standard GA
on two out of the four problems and better average
solutions on the remaining two. In one problem, the GA
successfully compressed 625 total bits of information into
a chromosome only 250 bits long by using alternative
reading frames. The authors label this behavior "extremely
sophisticated" and conclude that "These data show that a GA
can successfully use reading frames despite the added
complexity" and "It is clear that a GA can introduce new
'genes' as necessary to solve a given problem, even with
the difficulties imposed by using start and stop codons and
overlapping genes".
- GAs have preordained
goals
Like several others, this objection shows that Batten does
not fully understand what a genetic algorithm is and how it
works. He argues that GAs, unlike evolution, have goals
predetermined and specified at the outset, and as an
example of this, offers Dr. Richard Dawkins' "weasel"
program.
However, the weasel program is not a true genetic
algorithm, and is not typical of genetic algorithms, for
precisely that reason. It was not intended to demonstrate
the problem-solving power of evolution. Instead, its only
intent was to show the difference between single-step
selection (the infamous "tornado blowing through a junkyard
producing a 747") and cumulative, multi-step selection. It
did have a specific goal predetermined at the outset. True
genetic algorithms, however, do not.
In a broadly general sense, GAs do have a goal: namely, to
find an acceptable solution to a given problem. In this
same sense, evolution also has a goal: to produce organisms
that are better adapted to their environment and thus
experience greater reproductive success. But just as
evolution is a process without specific goals, GAs
do not specify at the outset how a given problem
should be solved. The fitness function is merely set up to
evaluate how well a candidate solution performs, without
specifying any particular way it should work and without
passing judgment on whatever way it does invent. The
solution itself then emerges through a process of mutation
and selection.
Batten's next statement shows clearly that he does not
understand what a genetic algorithm is. He asserts that
"Perhaps if the programmer could come up with a program
that allowed anything to happen and then measured the
survivability of the 'organisms', it might be getting
closer to what evolution is supposed to do" - but that
is exactly how genetic algorithms work. They
randomly generate candidate solutions and randomly mutate
them over many generations. No configuration is specified
in advance; as Batten puts it, anything is allowed to
happen. As John Koza (2003, p. 37)
writes, uncannily echoing Batten's words: "An important
feature... is that the selection [in genetic programming]
is not greedy. Individuals that are known to be inferior
will be selected to a certain degree. The best individual
in the population is not guaranteed to be selected.
Moreover, the worst individual in the population will not
necessarily be excluded. Anything can happen and nothing is
guaranteed." (An
earlier section discussed this very point as one of a
GA's strengths.) And yet, by applying a selective filter to
these randomly mutating candidates, efficient, complex and
powerful solutions to difficult problems arise, solutions
that were not designed by any intelligence and that can
often equal or outperform solutions that were
designed by humans. Batten's blithe assertion that "Of
course that is impossible" is squarely contradicted by
reality.
- GAs do not actually
generate new information
Batten's final criticism runs: "With a particular GA, we
need to ask how much of the 'information' generated by the
program is actually specified in the program, rather than
being generated de novo." He charges that GAs often do
nothing more than find the best way for certain modules to
interact when both the modules themselves and the ways they
can interact are specified ahead of time.
It is difficult to know what to make of this argument.
Any imaginable problem - terms in a calculus
equation, molecules in a cell, components of an engine,
stocks on a financial market - can be expressed in terms of
modules that interact in given ways. If all one has is
unspecified modules that interact in unspecified ways,
there is no problem to be solved. Does this mean that the
solution to no problem requires the generation of new
information?
In regards to Batten's criticism about information
contained in the solution being prespecified in the
problem, the best way to assuage his concerns is to point
out the many examples in which GAs begin with randomly
generated initial populations that are not in any way
designed to help the GA solve the problem. Some such
examples include: Graham-Rowe
2004; Davidson 1997; Assion et al. 1998; Giro, Cyrillo and Galvão 2002;
Glen and Payne 1995; Chryssolouris and Subramaniam
2001; Williams, Crossley and
Lang 2001; Robin et al. 2003;
Andreou, Georgopoulos and
Likothanassis 2002; Kewley and
Embrechts 2002; Rizki, Zmuda and
Tamburino 2002; and especially Koza
et al. 1999 and Koza et al.
2003, which discuss the use of genetic programming to
generate 36 human-competitive inventions in analog circuit
design, molecular biology, algorithmics, industrial
controller design, and other fields, all starting from
populations of randomly generated initial candidates.
Granted, some GAs do begin with intelligently generated
solutions which they then seek to improve, but this is
irrelevant: in such cases the aim is not just to return the
initially input solution, but to improve it by the
production of new information. In any case, even if the
initial situation is as Batten describes, finding the most
efficient way a number of modules can interact under a
given set of constraints can be a far from trivial task,
and one whose solution involves a considerable amount of
new information: scheduling at international airports, for
example, or factory assembly lines, or distributing casks
among warehouses and distilleries. Again, GAs have proven
themselves effective at solving problems whose complexity
would swamp any human. In light of the multiple innovations
and unexpectedly effective solutions arising from GAs in
many fields, Batten's claim that "The amount of new
information generated (by a GA) is usually quite trivial"
rings hollow indeed.
William Dembski
Old-earth creationist Dr. William Dembski's recent book,
No Free Lunch: Why Specified Complexity Cannot Be
Purchased Without Intelligence, is largely devoted to
the topic of evolutionary algorithms and how they relate to
biological evolution. In particular, Dembski's book is
concerned with an elusive quality he calls "specified
complexity," which he asserts is contained in abundance in
living things, and which he further asserts evolutionary
processes are incapable of generating, leaving "design"
through unspecified mechanisms by an unidentified
"intelligent designer" the only alternative. To bolster his
case, Dembski appeals to a class of mathematical theorems
known as the No Free Lunch theorems, which he claims prove
that evolutionary algorithms, on the average, do no better
than blind search.
Richard Wein has written an excellent and comprehensive
rebuttal to Dembski, entitled Not a Free Lunch But a Box of
Chocolates, and its points will not be reproduced here.
I will instead focus on chapter 4 of Dembski's book, which
deals in detail with genetic algorithms.
Dembski has one main argument against GAs, which is
developed at length throughout this chapter. While he does
not deny that they can produce impressive results - indeed,
he says that there is something "oddly compelling and
almost magical" (p.221) about the way GAs can find
solutions that are unlike anything designed by human beings
- he argues that their success is due to the specified
complexity that is "smuggled into" them by their human
designers and subsequently embodied in the solutions they
produce. "In other words, all the specified complexity we
get out of an evolutionary algorithm has first to be put
into its construction and into the information that guides
the algorithm. Evolutionary algorithms therefore do not
generate or create specified complexity, but merely harness
already existing specified complexity" (p.207).
The first problem evident in Dembski's argument is this.
Although his chapter on evolutionary algorithms runs for
approximately 50 pages, the first 30 of those pages discuss
nothing but Dr. Richard Dawkins' "weasel" algorithm, which,
as already discussed, is
not a true genetic algorithm and is not representative of
genetic algorithms. Dembski's other two examples - the
crooked wire genetic antennas of Edward Altshuler and Derek
Linden and the checkers-playing neural nets of Kumar
Chellapilla and David Fogel - are only introduced within
the last 10 pages of the chapter and are discussed for
three pages, combined. This is a serious deficiency,
considering that the "weasel" program is not representative
of most work being done in the field of evolutionary
computation; nevertheless, Dembski's arguments relating to
it will be analyzed.
In regard to the weasel program, Dembski states that
"Dawkins and fellow Darwinists use this example to
illustrate the power of evolutionary algorithms" (p.182),
and, again, "Darwinists... are quite taken with the
METHINKS IT IS LIKE A WEASEL example and see it as
illustrating the power of evolutionary algorithms to
generate specified complexity" (p.183). This is a straw
man of Dembski's creation (not least because Dawkins'
book was written long before Dembski ever coined that
term!). Here is what Dawkins really says about the purpose
of his program:
"What matters is the difference between the time taken
by cumulative selection, and the time which the same
computer, working flat out at the same rate, would take to
reach the target phrase if it were forced to use the other
procedure of single-step selection: about a million
million million million million years." (Dawkins 1996, p.49, emphasis
original)
In other words, the weasel program was intended to
demonstrate the difference between two different kinds of
selection: single-step selection, where a complex
result is produced by pure chance in a single leap, and
cumulative selection, where a complex result is
built up bit by bit via a filtering process that
preferentially preserves improvements. It was never
intended to be a simulation of evolution as a whole.
Single-step selection is the absurdly improbable process
frequently attacked in creationist literature by comparing
it to a tornado blowing through a junkyard producing a 747
airliner, or an explosion in a print shop producing a
dictionary. Cumulative selection is what evolution actually
uses. Using single-step selection to achieve a functional
result of any significant complexity, one would have to
wait, on average, many times the current age of the
universe. Using cumulative selection, however, that same
result can be reached in a comparatively very short length
of time. Demonstrating this difference was the point of
Dawkins' weasel program, and that was the only point
of that program. In a footnote to this chapter, Dembski
writes, "It is remarkable how Dawkins' example gets
recycled without any indication of the fundamental
difficulties that attend it" (p.230), but it is only
misconceptions in the minds of creationists such as Dembski
and Batten, who attack the weasel program for not
demonstrating something it was never intended to
demonstrate, that give rise to these "difficulties".
Unlike every example of evolutionary algorithms
discussed in this essay, the weasel program does indeed
have a single, prespecified outcome, and the quality of the
solutions it generates is judged by explicitly comparing
them to that prespecified outcome. Therefore, Dembski is
quite correct when he says that the weasel program does not
generate new information. However, he then makes a gigantic
and completely unjustified leap when he extrapolates this
conclusion to all evolutionary algorithms: "As the
sole possibility that Dawkins' evolutionary algorithm can
attain, the target sequence in fact has minimal
complexity.... Evolutionary algorithms are therefore
incapable of generating true complexity" (p.182). Even
Dembski seems to recognize this when he writes: "...most
evolutionary algorithms in the literature are programmed to
search a space of possible solutions to a problem until
they find an answer - not, as Dawkins does here, by
explicitly programming the answer into them in advance"
(p.182). But then, having given a perfectly good reason why
the weasel program is not representative of GAs as a whole,
he inexplicably goes on to make precisely that fallacious
generalization!
In reality, the weasel program is significantly
different from most genetic algorithms, and therefore
Dembski's argument from analogy does not hold up. True
evolutionary algorithms, such as the examples discussed in
this essay, do not simply find their way back to solutions
already discovered by other methods - instead, they are
presented with problems where the optimal solution is not
known in advance, and are asked to discover that solution
on their own. Indeed, if genetic algorithms could do
nothing more than rediscover solutions already programmed
into them, what would be the point of using them? It would
be an exercise in redundancy to do so. However, the
widespread scientific (and commercial) interest in GAs
shows that there is far more substance to them than the
rather trivial example Dembski tries to reduce this entire
field to.
Having set up and then knocked down this straw man,
Dembski moves on to his next line of argument: that the
specified complexity exhibited by the outcomes of more
representative evolutionary algorithms has, like the weasel
program, been "smuggled in" by the designers of the
algorithm. "But invariably we find that when specified
complexity seems to be generated for free, it has in fact
been front-loaded, smuggled in, or hidden from view"
(p.204). Dembski suggests that the most common "hiding
place" of specified complexity is in the GA's fitness
function. "What the [evolutionary algorithm] has done is
take advantage of the specified complexity inherent in the
fitness function and used it in searching for and then
locating the target..." (p.194). Dembski goes on to argue
that, before an EA can search a given fitness landscape for
a solution, some mechanism must first be employed to select
that fitness landscape from what he calls a phase
space of all the possible fitness landscapes, and if
that mechanism is likewise an evolutionary one, some other
mechanism must first be employed to select its
fitness function from an even larger phase space, and so
on. Dembski concludes that the only way to stop this
infinite regress is through intelligence, which he holds to
have some irreducible, mysterious ability to select a
fitness function from a given phase space without recourse
to higher-order phase spaces. "There is only one known
generator of specified complexity, and that is
intelligence" (p.207).
Dembski is correct when he writes that the fitness
function "guid[es] an evolutionary algorithm into the
target" (p.192). However, he is incorrect in his claim that
selecting the right fitness function is a process that
requires the generation of even more specified complexity
than the EA itself produces. As Koza (1999, p. 39) writes, the fitness
function tells an evolutionary algorithm "what needs to be
done", not "how to do it". Unlike the unrepresentative
weasel program example, the fitness function of an EA
typically does not specify any particular form that the
solution should take, and therefore it cannot be said to
contribute "specified complexity" to the evolved solution
in any meaningful sense.
An example will illustrate the point in greater detail.
Dembski claims that in Chellapilla and Fogel's checkers
experiment, their choice to hold the winning criterion
constant from game to game "inserted an enormous amount of
specified complexity" (p.223). It is certainly true that
the final product of this process displayed a great deal of
specified complexity (however one chooses to define that
term). But is it true that the chosen fitness measure
contained just as much specified complexity? Here is what
Chellapilla and Fogel actually say:
"To appreciate the level of play that has been achieved,
it may be useful to consider the following thought
experiment. Suppose you are asked to play a game on an
eight-by-eight board of squares with alternating colors.
There are 12 pieces on each side arranged in a specific
manner to begin play. You are told the rules of how the
pieces move (i.e., diagonally, forced jumps, kings) and
that the piece differential is available as a feature. You
are not, however, told whether or not this differential is
favorable or unfavorable (there is a version of checkers
termed 'suicide checkers,' where the object is to 'lose' as
fast as possible) or if it is even valuable information.
Most importantly, you are not told the object of the game.
You simply make moves and at some point an external
observer declares the game over. They do not, however,
provide feedback on whether or not you won, lost, or drew.
The only data you receive comes after a minimum of five
such games and is offered in the form of an overall point
score. Thus, you cannot know with certainty which games
contributed to the overall result or to what degree. Your
challenge is to induce the appropriate moves in each game
based only on this coarse level of feedback." (Chellapilla and Fogel 2001,
p.427)
It exceeds the bounds of the absurd for Dembski to claim
that this fitness measure inserted an "enormous" amount of
specified complexity. If a human being who had never heard
of checkers was given the same information, and we returned
several months later to discover that he had become an
internationally ranked checkers expert, should we conclude
that specified complexity has been generated?
Dembski states that to overturn his argument, "one must
show that finding the information that guides an
evolutionary algorithm to a target is substantially easier
than finding the target directly through a blind search"
(p.204). I contend that this is precisely the case.
Intuitively, it should not be surprising that the fitness
function contains less information than the evolved
solution. This is precisely the reason why GAs have found
such widespread use: it is easier (requires less
information) to write a fitness function that measures how
good a solution is, than to design a good solution from
scratch.
In more informal terms, consider Dembski's two examples,
the crooked-wire genetic antenna and the evolved
checkers-playing neural network named Anaconda. It requires
a great deal of detailed information about the game of
checkers to come up with a winning strategy (consider
Chinook and its enormous library of endgames). However, it
does not require equally detailed information to
recognize such a strategy when one sees it: all we need
observe is that that strategy consistently defeats its
opponents. Similarly, a person who knew nothing about how
to design an antenna that radiates evenly over a
hemispherical region in a given frequency range could still
test such an antenna and verify that it works as intended.
In both cases, determining what constitutes high
fitness is far easier (requires less information) than
figuring out how to achieve high fitness.
Granted, even though choosing a fitness function for a
given problem requires less information than actually
solving the problem defined by that fitness function, it
does take some information to specify the fitness
function in the first place, and it is a legitimate
question to ask where this initial information comes from.
Dembski may still ask about the origin of human
intelligence that enables us to decide to solve one problem
rather than another, or about the origin of the natural
laws of the cosmos that make it possible for life to exist
and flourish and for evolution to occur. These are valid
questions, and Dembski is entitled to wonder about them.
However, by this point - seemingly unnoticed by Dembski
himself - he has now moved away from his initial argument.
He is no longer claiming that evolution cannot happen;
instead, he is essentially asking why we live in a universe
where evolution can happen. In other words, what
Dembski does not seem to realize is that the logical
conclusion of his argument is theistic evolution. It
is fully compatible with a God who (as many Christians,
including evolutionary biologist Kenneth Miller, believe)
used evolution as his creative tool, and set up the
universe in such a way as to make it not just likely, but
certain.
I will conclude by clearing up some additional, minor
misconceptions in chapter 4 of No Free Lunch. For
starters, although Dembski, unlike Batten, is clearly aware
of the field of multiobjective optimization, he erroneously
states that "until some form of univalence is achieved,
optimization cannot begin" (p.186). This essay's discussion
of multiple-objective genetic algorithms shows the error of
this. Perhaps other design techniques have this
restriction, but one of the virtues of GAs is precisely
that they can make trade-offs and optimize several mutually
exclusive objectives simultaneously, and the human
overseers can then pick whichever solution best achieves
their goals from the final group of Pareto-optimal
solutions. No method of combining multiple criteria into
one is necessary.
Dembski also states that GAs "seem less adept at
constructing integrated systems that require multiple parts
to achieve novel functions" (p.237). The many examples
detailed in this essay (particularly John Koza's use of
genetic programming to engineer complex analog circuits)
show this claim to be false as well.
Finally, Dembski mentions that INFORMS, the professional
organization of the operations research community, pays
very little attention to GAs, and this "is reason to be
skeptical of the technique's general scope and power"
(p.237). However, just because a particular scientific
society is not making widespread use of GAs does not mean
that such uses are not widespread elsewhere or in general,
and this essay has endeavored to show that this is in fact
the case. Evolutionary techniques have found a wide variety
of uses in virtually any field of science one would care to
name, as well as among many companies in the
commercial sector. Here is a partial list:
By contrast, given the dearth of scientific discoveries
and research stimulated by intelligent design, Dembski is
in a poor position to complain about lack of practical
application. Intelligent design is a vacuous hypothesis,
telling us nothing more than "Some designer did something,
somehow, at some time, to cause this result." By contrast,
this essay has hopefully demonstrated that evolution is a
problem-solving strategy rich with practical
applications.
Even creationists find it impossible to deny that the
combination of mutation and natural selection can produce
adaptation. Nevertheless, they still attempt to justify
their rejection of evolution by dividing the evolutionary
process into two categories - "microevolution" and
"macroevolution" - and arguing that only the second is
controversial, and that any evolutionary change we observe
is only an example of the first.
Now, microevolution and macroevolution are terms
that have meaning to biologists; they are defined,
respectively, as evolution below the species level and
evolution at or above the species level. But the crucial
difference between the way creationists use these terms and
the way scientists use them is that scientists recognize
that these two are fundamentally the same process with the
same mechanisms, merely operating at different scales.
Creationists, however, are forced to postulate some type of
unbridgeable gap separating the two, in order for them to
deny that the processes of change and adaptation we see
operating in the present can be extrapolated to produce all
the diversity observed in the living world.
However, genetic algorithms make this view untenable by
demonstrating the fundamental seamlessness of the
evolutionary process. Take, for example, a problem that
consists of programming a circuit to discriminate between a
1-kilohertz and a 10-kilohertz tone, and respond
respectively with steady outputs of 0 and 5 volts. Say we
have a candidate solution that can accurately discriminate
between the two tones, but its outputs are not quite steady
as required; they produce small waveforms rather than the
requisite unchanging voltage. Presumably, according to the
creationist view, to change this circuit from its present
state to the perfect solution would be "microevolution", a
small change within the ability of mutation and selection
to produce. But surely, a creationist would argue, to
arrive at this same final state from a completely random
initial arrangement of components would be "macroevolution"
and beyond the reach of an evolutionary process. However,
genetic algorithms were able to accomplish both, evolving
the system from a random arrangement to the near-perfect
solution and finally to the perfect, optimal solution. At
no step of the way did an insoluble difficulty or a gap
that could not be bridged turn up. At no point whatsoever
was human intervention required to assemble an irreducibly
complex core of components (despite the fact that the
finished product does contain such a thing) or to "guide"
the evolving system over a difficult peak. The circuit
evolved, without any intelligent guidance, from a
completely random and non-functional state to a tightly
complex, efficient and optimal state. How can this
not be a compelling experimental demonstration of
the power of evolution?
It has been said that human cultural evolution has
superceded the biological kind - that we as a species have
reached a point where we are able to consciously control
our society, our environment and even our genes to a
sufficient degree to make the evolutionary process
irrelevant. It has been said that the cultural whims of our
rapidly changing society, rather than the comparatively
glacially slow pace of genetic mutation and natural
selection, is what determines fitness today. In a sense,
this may well be true.
But in another sense, nothing could be further from the
truth. Evolution is a problem-solving process whose power
we are only beginning to understand and exploit; despite
this, it is already at work all around us, shaping our
technology and improving our lives, and in the future,
these uses will only multiply. Without a detailed
understanding of the evolutionary process, none of the
countless advances we owe to genetic algorithms would have
been possible. There is a lesson here to those who deny the
power of evolution, as well as those who deny that
knowledge of it has any practical benefit. As incredible as
it may seem, evolution works. As the poet Lord Byron
put it: "'Tis strange but true; for truth is always
strange, stranger than fiction."
"Adaptive Learning: Fly the Brainy Skies." Wired,
vol.10, no.3 (March 2002). Available online at
http://www.wired.com/wired/archive/10.03/everywhere.html?pg=2.
Altshuler, Edward and Derek Linden. "Design of a wire
antenna using a genetic algorithm." Journal of
Electronic Defense, vol.20, no.7, p.50-52 (July
1997).
Andre, David and
Astro Teller. "Evolving team Darwin United." In
RoboCup-98: Robot Soccer World Cup II, Minoru Asada
and Hiroaki Kitano (eds). Lecture Notes in Computer
Science, vol.1604, p.346-352. Springer-Verlag, 1999.
Andreou, Andreas, Efstratios Georgopoulos and Spiridon
Likothanassis. "Exchange-rates forecasting: A hybrid
algorithm based on genetically optimized adaptive neural
networks." Computational Economics, vol.20, no.3,
p.191-210 (December 2002).
Ashley, Steven. "Engineous explores the design space."
Mechanical Engineering, February 1992, p.49-52.
Assion, A., T. Baumert, M. Bergt, T. Brixner, B. Kiefer,
V. Seyfried, M. Strehle and G. Gerber. "Control of chemical
reactions by feedback-optimized phase-shaped femtosecond
laser pulses." Science, vol.282, p.919-922 (30
October 1998).
Au, Wai-Ho, Keith Chan, and Xin Yao. "A novel
evolutionary data mining algorithm with applications to
churn prediction." IEEE Transactions on Evolutionary
Computation, vol.7, no.6, p.532-545 (December
2003).
Beasley, J.E., J. Sonander and P. Havelock. "Scheduling
aircraft landings at London Heathrow using a population
heuristic." Journal of the Operational Research
Society, vol.52, no.5, p.483-493 (May 2001).
Begley, Sharon and Gregory Beals. "Software au naturel."
Newsweek, May 8, 1995, p.70.
Benini, Ernesto and Andrea Toffolo. "Optimal design of
horizontal-axis wind turbines using blade-element theory
and evolutionary computation." Journal of Solar Energy
Engineering, vol.124, no.4, p.357-363 (November
2002).
Burke, E.K. and J.P. Newall. "A multistage evolutionary
algorithm for the timetable problem." IEEE Transactions
on Evolutionary Computation, vol.3, no.1, p.63-74
(April 1999).
Charbonneau, Paul. "Genetic algorithms in astronomy and
astrophysics." The Astrophysical Journal Supplement
Series, vol.101, p.309-334 (December 1995).
Chellapilla, Kumar and David Fogel. "Evolving an expert
checkers playing program without using human expertise."
IEEE Transactions on Evolutionary Computation,
vol.5, no.4, p.422-428 (August 2001). Available online at
http://www.natural-selection.com/NSIPublicationsOnline.htm.
Chellapilla, Kumar and David Fogel. "Anaconda defeats
Hoyle 6-0: a case study competing an evolved checkers
program against commercially available software." In
Proceedings of the 2000 Congress on Evolutionary
Computation, p.857-863. IEEE Press, 2000. Available
online at
http://www.natural-selection.com/NSIPublicationsOnline.htm.
Chellapilla, Kumar and David Fogel. "Verifying
Anaconda's expert rating by competing against Chinook:
experiments in co-evolving a neural checkers player."
Neurocomputing, vol.42, no.1-4, p.69-86 (January
2002).
Chryssolouris, George and Velusamy Subramaniam. "Dynamic
scheduling of manufacturing job shops using genetic
algorithms." Journal of Intelligent Manufacturing,
vol.12, no.3, p.281-293 (June 2001).
Coale, Kristi. "Darwin in a box." Wired News,
July 14, 1997. Available online at
http://www.wired.com/news/technology/0,1282,5152,00.html.
Coello, Carlos. "An updated survey of GA-based
multiobjective optimization techniques." ACM Computing
Surveys, vol.32, no.2, p.109-143 (June 2000).
Davidson, Clive. "Creatures from primordial silicon."
New Scientist, vol.156, no.2108, p.30-35 (November
15, 1997). Available online at
http://www.newscientist.com/hottopics/ai/primordial.jsp.
Dawkins, Richard. The Blind Watchmaker: Why the
Evidence of Evolution Reveals a Universe Without
Design. W.W. Norton, 1996.
Dembski, William. No Free Lunch: Why Specified
Complexity Cannot Be Purchased Without Intelligence.
Rowman & Littlefield, 2002.
Fleming, Peter and R.C. Purshouse. "Evolutionary
algorithms in control systems engineering: a survey."
Control Engineering Practice, vol.10, p.1223-1241
(2002).
Fonseca, Carlos
and Peter Fleming. "An overview of evolutionary algorithms
in multiobjective optimization."
Evolutionary
Computation, vol.3, no.1, p.1-16 (1995).
Forrest, Stephanie. "Genetic algorithms: principles of
natural selection applied to computation." Science,
vol.261, p.872-878 (1993).
Gibbs, W. Wayt. "Programming with primordial ooze."
Scientific American, October 1996, p.48-50.
Gillet, Valerie. "Reactant- and product-based approaches
to the design of combinatorial libraries." Journal of
Computer-Aided Molecular Design, vol.16, p.371-380
(2002).
Giro, R., M. Cyrillo and D.S. Galvão. "Designing
conducting polymers using genetic algorithms." Chemical
Physics Letters, vol.366, no.1-2, p.170-175 (November
25, 2002).
Glen, R.C. and A.W.R. Payne. "A genetic algorithm for
the automated generation of molecules within constraints."
Journal of Computer-Aided Molecular Design, vol.9,
p.181-202 (1995).
Goldberg, David. Genetic Algorithms in Search,
Optimization, and Machine Learning. Addison-Wesley,
1989.
Graham-Rowe, Duncan. "Radio emerges from the electronic
soup." New Scientist, vol.175, no.2358, p.19 (August
31, 2002). Available online at
http://www.newscientist.com/news/news.jsp?id=ns99992732.
- See also: Bird, Jon and Paul Layzell. "The evolved
radio and its implications for modelling the evolution of
novel sensors." In Proceedings of the 2002 Congress on
Evolutionary Computation, p.1836-1841.
Graham-Rowe, Duncan. "Electronic circuit 'evolves' from
liquid crystals." New Scientist, vol.181, no.2440,
p.21 (March 27, 2004).
Haas, O.C.L., K.J. Burnham and J.A. Mills. "On improving
physical selectivity in the treatment of cancer: A systems
modelling and optimisation approach." Control
Engineering Practice, vol.5, no.12, p.1739-1745
(December 1997).
Hanne, Thomas. "Global multiobjective optimization using
evolutionary algorithms." Journal of Heuristics,
vol.6, no.3, p.347-360 (August 2000).
Haupt, Randy and Sue Ellen Haupt. Practical Genetic
Algorithms. John Wiley & Sons, 1998.
He, L. and N. Mort. "Hybrid genetic algorithms for
telecommunications network back-up routeing." BT
Technology Journal, vol.18, no.4, p. 42-50 (Oct
2000).
Holland, John. "Genetic algorithms." Scientific
American, July 1992, p. 66-72.
Hughes, Evan and Maurice Leyland. "Using multiple
genetic algorithms to generate radar point-scatterer
models." IEEE Transactions on Evolutionary
Computation, vol.4, no.2, p.147-163 (July 2000).
Jensen, Mikkel. "Generating robust and flexible job shop
schedules using genetic algorithms." IEEE Transactions
on Evolutionary Computation, vol.7, no.3, p.275-288
(June 2003).
Kewley, Robert and Mark Embrechts. "Computational
military tactical planning system." IEEE Transactions on
Systems, Man and Cybernetics, Part C - Applications and
Reviews, vol.32, no.2, p.161-171 (May 2002).
Kirkpatrick, S., C.D. Gelatt and M.P. Vecchi.
"Optimization by simulated annealing." Science,
vol.220, p.671-678 (1983).
Koza, John, Forest Bennett, David Andre and Martin
Keane. Genetic Programming III: Darwinian Invention and
Problem Solving. Morgan Kaufmann Publishers, 1999.
Koza, John, Martin
Keane, Matthew Streeter, William Mydlowec, Jessen Yu and
Guido Lanza.
Genetic Programming IV: Routine
Human-Competitive Machine Intelligence. Kluwer Academic
Publishers, 2003.
- See also: Koza, John, Martin Keane and Matthew
Streeter. "Evolving inventions." Scientific
American, February 2003, p. 52-59.
Keane, A.J. and S.M. Brown. "The design of a satellite
boom with enhanced vibration performance using genetic
algorithm techniques." In Adaptive Computing in
Engineering Design and Control '96 - Proceedings of the
Second International Conference, I.C. Parmee (ed),
p.107-113. University of Plymouth, 1996.
Lee, Yonggon and Stanislaw H. Zak. "Designing a genetic
neural fuzzy antilock-brake-system controller." IEEE
Transactions on Evolutionary Computation, vol.6, no.2,
p.198-211 (April 2002).
Lemley, Brad. "Machines that think." Discover,
January 2001, p.75-79.
Mahfoud, Sam and Ganesh Mani. "Financial forecasting
using genetic algorithms." Applied Artificial
Intelligence, vol.10, no.6, p.543-565 (1996).
Mitchell, Melanie. An Introduction to Genetic
Algorithms. MIT Press, 1996.
Naik, Gautam. "Back to Darwin: In sunlight and cells,
science seeks answers to high-tech puzzles." The Wall
Street Journal, January 16, 1996, p. A1.
Obayashi, Shigeru, Daisuke Sasaki, Yukihiro Takeguchi,
and Naoki Hirose. "Multiobjective evolutionary computation
for supersonic wing-shape optimization." IEEE
Transactions on Evolutionary Computation, vol.4, no.2,
p.182-187 (July 2000).
Petzinger, Thomas. "At Deere they know a mad scientist
may be a firm's biggest asset." The Wall Street
Journal, July 14, 1995, p.B1.
Porto, Vincent, David Fogel and Lawrence Fogel.
"Alternative neural network training methods." IEEE
Expert, vol.10, no.3, p.16-22 (June 1995).
Rao, Srikumar. "Evolution at warp speed." Forbes,
vol.161, no.1, p.82-83 (January 12, 1998).
Rizki, Mateen, Michael Zmuda and Louis Tamburino.
"Evolving pattern recognition systems." IEEE
Transactions on Evolutionary Computation, vol.6, no.6,
p.594-609 (December 2002).
Robin, Franck, Andrea Orzati, Esteban Moreno, Otte
Homan, and Werner Bachtold. "Simulation and evolutionary
optimization of electron-beam lithography with genetic and
simplex-downhill algorithms." IEEE Transactions on
Evolutionary Computation, vol.7, no.1, p.69-82
(February 2003).
Sagan, Carl. Broca's Brain: Reflections on the
Romance of Science. Ballantine, 1979.
Sambridge, Malcolm and Kerry Gallagher. "Earthquake
hypocenter location using genetic algorithms." Bulletin
of the Seismological Society of America, vol.83, no.5,
p.1467-1491 (October 1993).
Sasaki, Daisuke, Masashi Morikawa, Shigeru Obayashi and
Kazuhiro Nakahashi. "Aerodynamic shape optimization of
supersonic wings by adaptive range multiobjective genetic
algorithms." In Evolutionary Multi-Criterion
Optimization: First International Conference, EMO 2001,
Zurich, Switzerland, March 2001: Proceedings, K. Deb,
L. Theile, C. Coello, D. Corne and E. Zitler (eds). Lecture
Notes in Computer Science, vol.1993, p.639-652.
Springer-Verlag, 2001.
Sato, S., K. Otori, A. Takizawa, H. Sakai, Y. Ando and
H. Kawamura. "Applying genetic algorithms to the optimum
design of a concert hall." Journal of Sound and
Vibration, vol.258, no.3, p. 517-526 (2002).
Schechter, Bruce. "Putting a Darwinian spin on the
diesel engine." The New York Times, September 19,
2000, p. F3.
Srinivas, N. and Kalyanmoy Deb. "Multiobjective
optimization using nondominated sorting in genetic
algorithms." Evolutionary Computation, vol.2, no.3,
p.221-248 (Fall 1994).
Soule, Terrence and Amy Ball. "A genetic algorithm with
multiple reading frames." In GECCO-2001: Proceedings of
the Genetic and Evolutionary Computation Conference,
Lee Spector and Eric Goodman (eds). Morgan Kaufmann, 2001.
Available online at
http://www.cs.uidaho.edu/~tsoule/research/papers.html.
Tang, K.S., K.F. Man, S. Kwong and Q. He. "Genetic
algorithms and their applications." IEEE Signal
Processing Magazine, vol.13, no.6, p.22-37 (November
1996).
Weismann, Dirk, Ulrich Hammel, and Thomas Bäck.
"Robust design of multilayer optical coatings by means of
evolutionary algorithms." IEEE Transactions on
Evolutionary Computation, vol.2, no.4, p.162-167
(November 1998).
Williams, Edwin, William Crossley and Thomas Lang.
"Average and maximum revisit time trade studies for
satellite constellations using a multiobjective genetic
algorithm." Journal of the Astronautical Sciences,
vol.49, no.3, p.385-400 (July-September 2001).
Zitzler, Eckart and Lothar Thiele. "Multiobjective
evolutionary algorithms: a comparative case study and the
Strength Pareto approach." IEEE Transactions on
Evolutionary Computation, vol.3, no.4, p.257-271
(November 1999).
